ADS
1.Advanced Data Structure
1.1 Tree
1.1.1 AVL Tree
目标:加快搜索速度
定义:
- 空的树是height balanced的(左右子树的高度差绝对值不超过1)
- 左右子树的高度差为-1、0、1
- 高度height:空树height=-1,单节点为0
- 平衡因子:\(BF(Node)=H_{L}-H_{R}\)
- 因此平衡树的平衡因子为-1,0,1
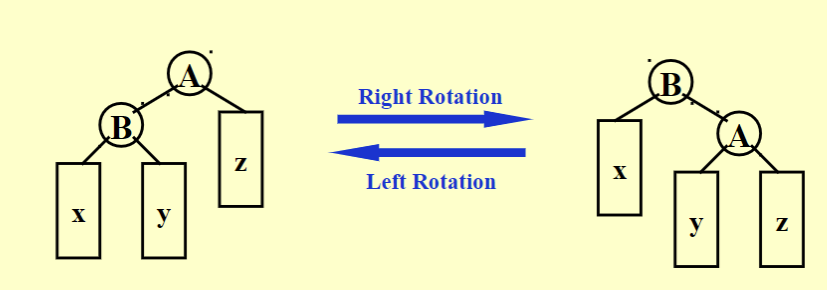
树的旋转Rotation
当高度差打破平衡使用旋转,旋转是不改变大小顺序关系的,旋转有LL、RR、LR、RL四种方式,基本是左右旋的组合使用
右旋Right Rotation
左旋Left Rotation
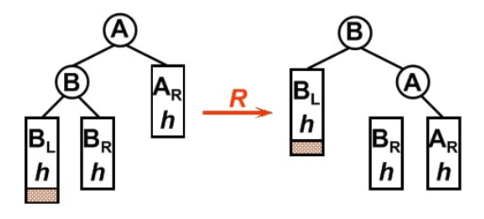
LL型旋转
插入的节点在不平衡点的左节点的左子树中,此时是LL型,对不平衡点使用一次右旋
1
if(isLL){RightRotation(WrongNode);}
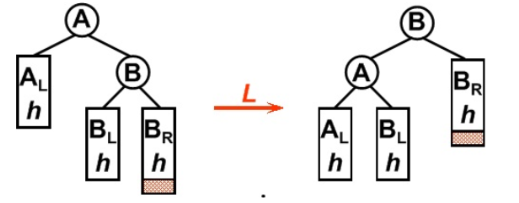
RR型旋转
插入的节点在不平衡点的右节点的右子树中,此时是RR型,对不平衡点使用一次左旋
1
if(isRR){LeftRotation(WrongNode);}
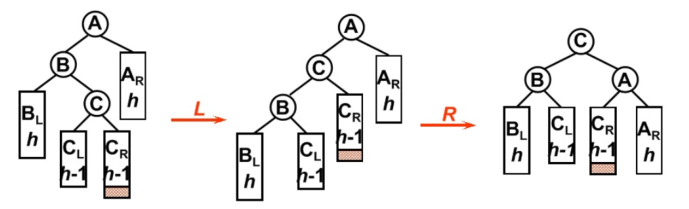
LR型旋转
插入的节点在不平衡点的左节点的右子树中,此时是LR型,先对WrongNode->Left进行一次左旋,再对WrongNode进行一次右旋
1
2
3
4if(isLR){
LeftRotation(WrongNode->Left);
RightRotation(WrongNode);
}
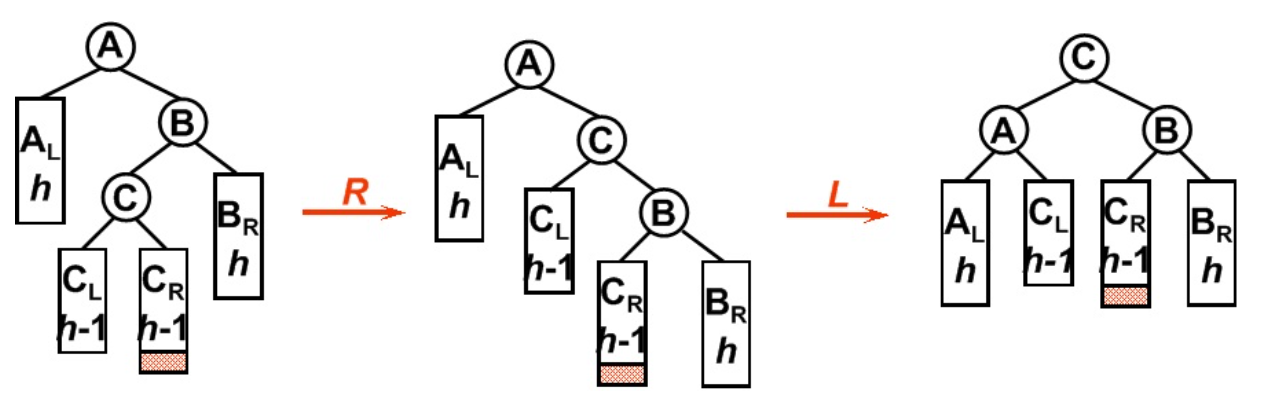
RL型旋转
插入的节点在不平衡点的右节点的左子树中,此时是LR型,先对WrongNode->Right进行一次右旋,再对WrongNode进行一次左旋
1
2
3
4if(isRL){
RightRotation(WrongNode->Right);
LeftRotation(WrongNode);
}
对于高度为h的树,最少节点个数为\(n_{h}\),\(n_{k}\)的递推关系式为
\(n_{h}=n_{h-1}+n_{h-2}+1\)
\((n_{h}+1)=(n_{h-1}+1)+(n_{h-2}+1)\)
注意到斐波那契数列的递推式
\(F_{n}=F_{n-1}+F_{n-2}\)
修改一下初项,即可得到
\(n_{h}=F_{h+2}-1\)
\(F_i=\frac{1}{\sqrt{5}\ }(\frac{1+\sqrt{5}\ }{2})^i\)
则\(h→O(lnN)\)
1.1.2 Splay Tree
目标:从空树开始,任何M次连续操作一共最多消耗\(O(MlogN)\)的时间
- 必须从空树开始
- 具体做法:在树中,每次有节点被访问到,就旋转节点到树根
旋转方法:
如果父节点是Root,直接父子旋转
如果父节点不是Root
Zig-Zag(之字形)
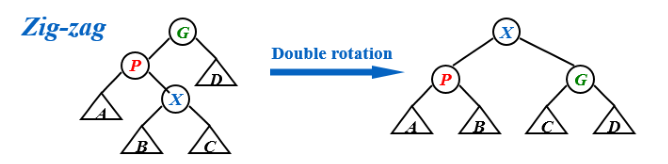
1
2
3
4if(isZig_Zag){
LeftRotation(P);
RightRotation(G);
}Zig-Zig(线形)
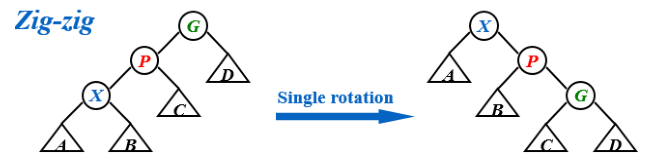
1
2
3
4if(isZig_Zig){
RightRotation(G);
RightRotation(P);
}
按照上述规则将X节点转到Root节点即可
删除方法:
- Find(X),此时X到了Root的位置
- 删除根节点,得到左右子树
- FindMax(\(T_{L}\))作为根节点,将右子树接上
【补充】代价计算
Worst Case 最差情况的计算
Amortized case 均摊代价:与数据分布无关,即对一个序列的所有操作取平均,均摊分析的结果可能是最坏情况也可能是平均情况。
average case 平均代价:简单地把每一个操偶做的单独代价加起来取平均。
- 比如a,b,c操作要1,2,3分钟,那么平均代价就是2,但是对于序列操作abcc,均摊代价是2.25。
- Worst case >= Amortized case >=average case
【补充】均摊代价的分析
聚集分析法
证明对所有的n,由n个操作所构成的序列的总时间在最坏情况下的T(N),每一个操作的代价就是\(\frac{T(N)}{N}\),比如栈的操作push、pop、mutipop,sizeof(S)<=n,那么总的时间最大为O(n),则均摊代价为O(1)。
记账法
amortized cost 为\(\overline{c_i}\)
actual cost 为\({c_i}\)
credit 为amortized cost-actual cost,
credit可以pay for later operations
要保证credit>=0!!!
O(n)=\(\sum{\overline{c_i}\ }≥\sum c_i\)
\(T_{amortized}=O(n)/n\)
如栈操作中,T(n)=push+pop(实际代价)<=2push(amortized cost)<=2n=O(n)
这里我们把push的代价设置为了2,实际是1,pop的代价是0实际是1
势能法
\(\overline{c_i}-c_i=Credit_i=\Phi(D_i)-\Phi(D_{i-1})\)
\(\sum{\overline{c_i}\ }=\sum (c_i+\Phi(D_i)-\Phi(D_{i-1}))=(\sum c_i)+\Phi(D_n)-\Phi(D_{0})\)
这里的\(\Phi(D_i)\)为势能函数,\(D_i\)是i次操作后的某种状态
要保证,在D0时势能最小
如栈操作中,我们设置势能函数为栈的size那么首先D0时为0
由于push的数量大于等于pop,那么\(\Phi(D_i)≥0\)
那么\(\sum{\overline{c_i}\ }=O(n)≥\sum c_i\)
1.1.3 红黑树
定义:
- 红黑树是一种BST,节点具有颜色红色(0)或者黑色(1)
- 红黑树的根节点是黑色
- 叶节点为黑色,叶节点为NULL时,把NULL也视作黑色的节点
- 红节点的两个儿子一定是黑节点
- 对于每一个节点,从该节点出发到后代的叶节点的简单路径包含的黑节点数量相同
黑高(Black Height of Node x)
- bh(x)表示从x到叶节点的路径中的黑节点个数,不含节点自身
- 性质:
- N个节点,高度最多为\(2ln(N+1)\)
- sizeof(x)≥\(2^{bh(x)}-1\)(可以归纳证明)
- \(bh(Tree)≥\frac{h(Tree)}{2}\)
红黑树的操作:
插入:
将节点染红插入BST,可能破坏性质2、4
判断旋转方式:
case1:叔节点为红色
则将父节点和叔节点变为黑色,祖父节点变为红色,祖父继续视作插入点向上迭代
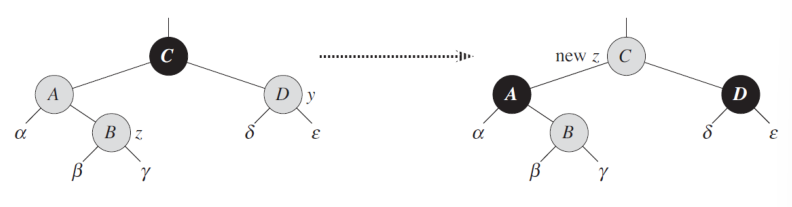
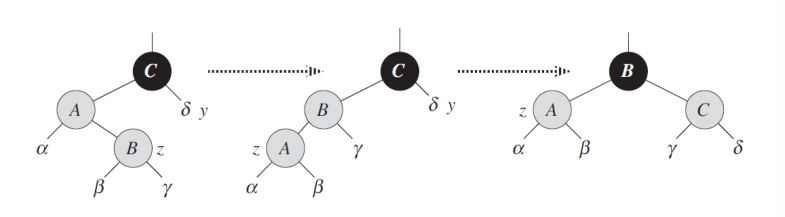
case2:叔节点为黑色
将插入节点转为远侄子,再转为case1,如图
删除
- 删除的节点是叶节点:直接让其父节点指向NULL
- 删除的节点度数为1:用孩子代替这个节点
- 删除的节点度数为2:用最大左儿子或者最小右儿子代替
- 当删除节点为红色,性质不会被破坏,若删除的节点是黑色,则性质会被破坏
删除的具体操作
设v是要删除的节点,u是替代v的节点,u可能是NULL,是NULL的话,当作黑色处理。
删除操作总纲: 执行标准的 BST 的删除操作 简单情况:u 或者 v 是红色 复杂情况:u 和 v 都是黑色结点。引入双黑节点
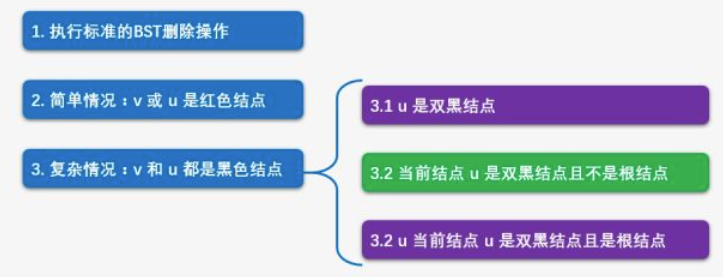
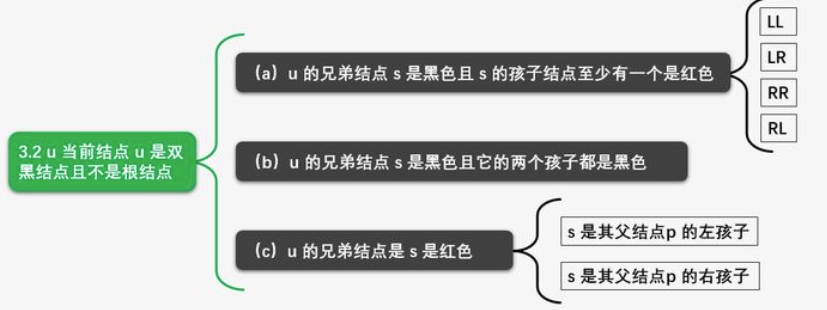
双黑节点的删除情况
我们用数值表示颜色,更好理解,0为红色,-1、1为黑色,2为双黑
case1:兄弟节点s为红色
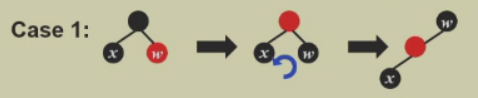
s与p交换颜色,且把s转上来
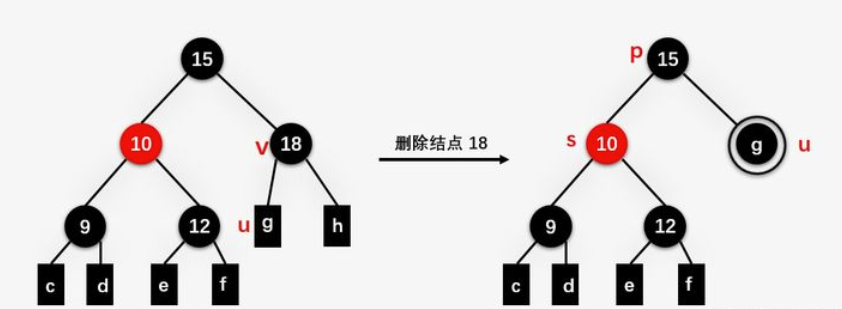
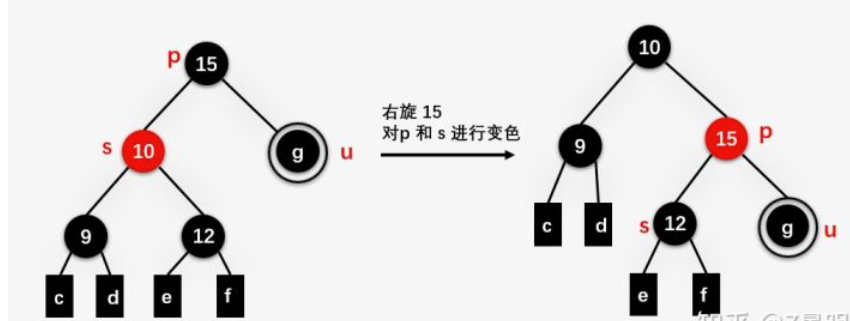
到case2
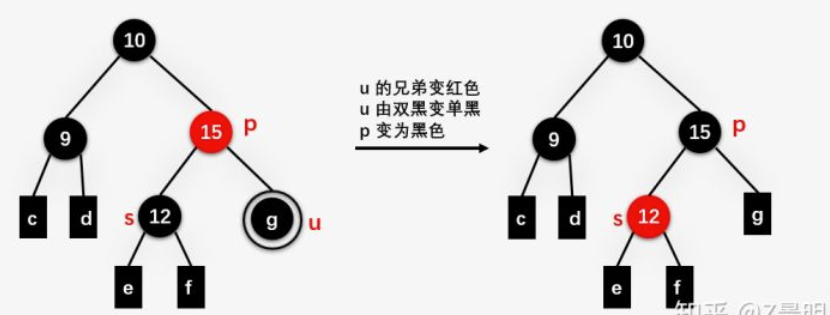
case2:兄弟节点s为黑色,侄子(s的儿子)均为黑
u和s颜色减1,p的颜色加1

如果p加完1是黑色则结束了
如果p加完1是双黑
 alt="image-20220306161733293" style="zoom:60%;" />
alt="image-20220306161733293" style="zoom:60%;" />
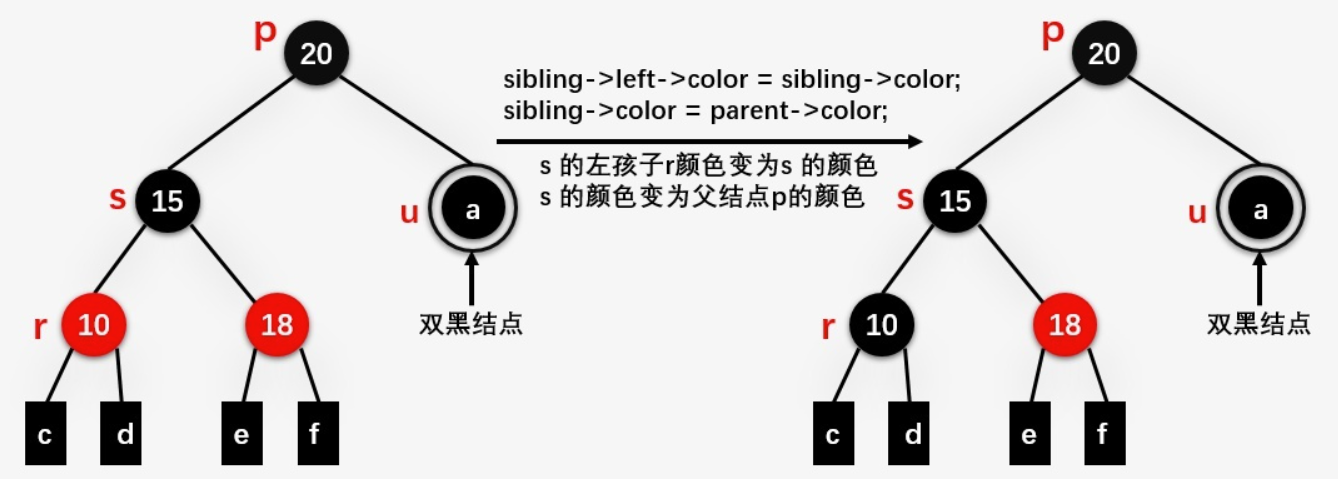
case3:兄弟节点s为黑色,侄子至少一个红色
u和s的父亲p节点,s的红孩子设为r,则查看p、s、r的关系,若有两个红孩子,优先查看LL、RR型:
LL: s的颜色变成p的颜色,r的颜色变成s的颜色
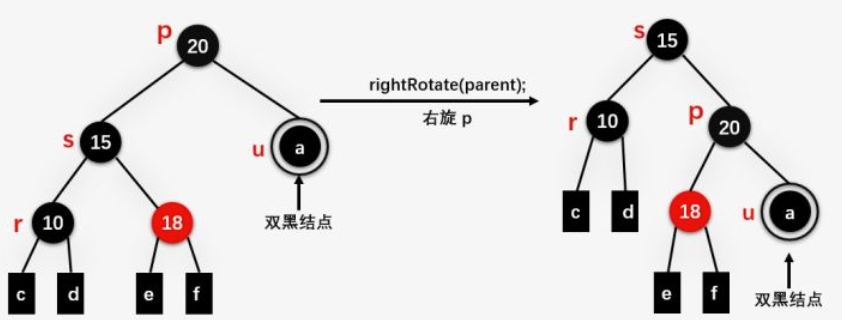
旋转p节点
 p设置为黑色,双黑变成单黑
p设置为黑色,双黑变成单黑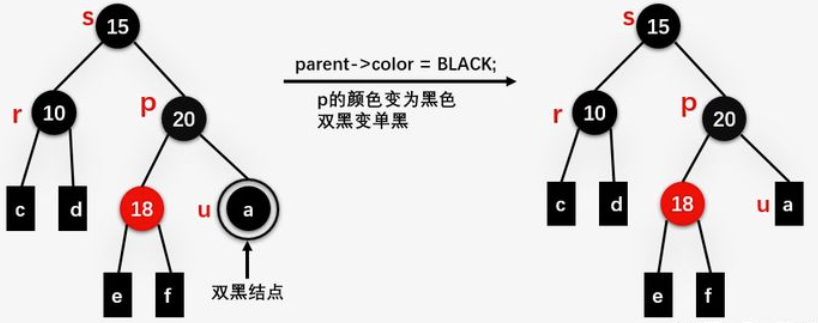
当为LR、RL型时,转化为LL、RR型:
s变为红色,r变为黑色,旋转s,变成LL、RR型
1.1.4 B+树
M阶的B+树定义:
- 根节点是叶节点或者根节点有2~M个儿子
- 根之外的非叶节点有\([\frac{M}{2}]\)M个儿子,每个叶节点有\([\frac{M}{2}]\)M个元素//这里与数据库里的不同
- B+树的儿子指的是节点指向的新节点而非节点内的数据
- 每个节点的 key数是子节点数-1,画图的时候key分布在指向两个儿子的箭头之间
- key值的确定方法:等于key右边第一个指针对应子节点的最左边的值
- 所有叶节点的深度相同
- B+ Tree of Order 4 也称为2-3-4树,order 3 的称为2-3树
B+树的插入算法
对于order M, 有N个元素的B+树而言\(T=O(\frac{M}{logM}logN)\)
B+树的深度Depth(M,N)=\(O([log_{M/2}N])\), 找到插入位置的事件复杂度是log N
对于order3的B+树而言,非叶节点的索引个数在有三个儿子时需要两个,否则只需要一个索引
```cpp Btree Insert ( ElementType X, Btree T ) { Search from root to leaf for X and find the proper leaf node; Insert X; while ( this node has M+1 keys ) { split it into 2 nodes with [(M+1)/2] and [(M+1)/2] keys, respectively; if (this node is the root) create a new root with two children; check its parent; } } //算法的描述:找到合适的位置先插入,如果叶节点的keys数量超过了M,则分裂成两个,然后向上继续合并和拆分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
- Deletion is similar to insertion except that the root is removed when it loses two
children 删除和插入的做法相似,不过当一个根节点失去两个儿子时就要删除
### 1.2 Invert File Index
- 文档关联矩阵 Term-Document incidence Matrix
- a matrix of appearance of each word in each doc。
- 某个单词在某篇中出现,则矩阵对应位置上为1,否则为0,若干篇文章的出现情况可以都得到若干个二进制字符串
- 只关注单词的出现与否,不关注频率
- 矩阵比较稀疏
- **用逻辑运算可以考察多个单词在doc中出现的情况**
- 倒排文件索引 Invert File Index
- 一种在文章中定位单词的方法。
- **看词在哪些文章中出现了**
- 索引方法:
1. 单词--<次数;出现单词的doc编号>
2. 单词--<次数;(doc号;位置1;位置2;…),…<img src = "ADS笔记\image-20220328193119874.png"> alt="image-20220328193119874" style="zoom:67%;" />
- 索引生成器:
```pseudocode
while(read a document D){
while(read a term T in D){
if(Find(Dictionary,T)==false)
Insert(T);
Get T's position list;
Insert a node to T's posting list
}
}
write the inverted index to disk
读取的简单处理
- 碰到一个单词的多种形态要统一,如过去式、将来时、现在式
- 频率高但是无实际意义的单词无需统计,如a、the
当储存空间不足时的措施
- 采用多块内存储存
- 分布式索引:
- 按单词的首字母划分
- 按文档的编号划分(更好,抗风险)
- 动态索引:
- 不常用的索引会删除
- 索引由main index+auxiliary index组成
阈值Thresholding
- document:直接检索前面X个按权重排序的文档
- 对于布尔查询无效
- 会遗漏重要文档,因为有截断
- query:把带查询的terms按照出现的频率排序
- document:直接检索前面X个按权重排序的文档
搜索引擎的评价:
- 索引创建多快 how fast does it index
- 搜索有多快 how fast does it search
- 查询语言的表现 Expressiveness of query language
Data Retrieval Performance
- Response time
- Index Space
Information Retrieval Performance
- How relevant is the answer set?
Relevance measurement
准确率precision
\(P=\frac{R_R}{R_R+I_R}\)
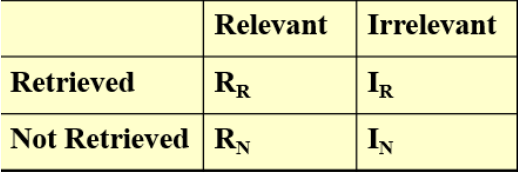
召回率 recall
$R=
 alt="image-20220328194318411" style="zoom:67%;" />
alt="image-20220328194318411" style="zoom:67%;" />
【习题】While accessing a term, hashing is faster than search trees.
答:True,因为hash表是直接使用hash函数定位的时间是常数的,而使用搜索树则是O(logn)的。但是hash表的储存不灵活有缺点。
【习题】In distributed indexing, document-partitioned strategy is to store on each node all the documents that contain the terms in a certain range.
答:False,因为分布式索引的方式是按文档序号排序的,如果按包含的terms分类,在储存故障时,关于这个terms的文档全没了,不抗风险。
【习题】When evaluating the performance of data retrieval, it is important to measure the relevancy of the answer set.
答:False,这个说的是data retrieval,错。Information retrieval才需要measure the relevancy of the answer set。
【习题】Precision is more important than recall when evaluating the explosive detection in airport security.
答:False,在机场安全的危险品探测中应该是Recall率更重要。
1.3 Heap
1.3.1 Leftist Heap 左倾堆
NPL(X)--NULL Path Length
- 对任意一个节点X,通往一个没有两个子节点(外节点)的最短路径长度,空节点的NPL值为-1,外节点的NPL为0;
- 计算方法:\(NPL(X)=min \{NPL(c)|c\ is\ a\ child\ of\ X\}+1\)
左倾堆的性质:
对每一个节点,左儿子的NPL不小于右儿子的NPL值,整体看起来向左倾斜
左倾堆的本质是一种不平衡的二叉树,它的数据结构定义如下
1
2
3
4
5
6struct TreeNode{
ElementType Element;
PriorityQueue Left;
PriorityQueue Right;
int Npl;
};对于一个右路径有 \(r\) 个节点的左倾堆,至少一共有个\(2^r-1\)节点【归纳证明】
有N个节点的左倾树,右路径最多\(\lfloor log(N+1) \rfloor\)个节点,启发我们在右路经上进行操作
左倾堆的合并
递归方法:
每次合并比较左倾堆的根节点大小,大的合并在小的上面,并且根据NPL交换左右
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17PriorityQueue Merge(PriorityQueue H1,PriorityQueue H2){
if(H1==NULL) return H2;
if(H2==NULL) return H1;
if(H1->Element<H2->Element) return Merge1(H1,H2);
else return Merge1(H2,H1);
}
PriorityQueue Merge1(PriorityQueue H1,PriorityQueue H2){
if(H1->Left == NULL)//single node
H1->Left = H2;//H1->Right is already NULL
else{
H1->Right = Merge(H1->Right,H2);
if(H1->Left->Npl<H1->Right->Npl)
SwapChildren(H1);
H1->Npl = H1->Right->Npl + 1;
}
return H1;
}迭代方法
对所有的右路径上的节点排序,且不改变左儿子
根据NPL交换左右。
左倾堆的删除
- 删除最小的,即根节点
- 合并两颗剩下的子树
- \(T_p=O(logN)\)
1.3.2 Skew Heap斜堆
- 目的:从空触发,M次操作的总时间为\(O(MlogN)\)
- 无NPL的限制,合并后左右子树一定交换!
- 插入:为特殊的合并。
- 合并:每一次Merge完都要交换左右子树
- 删除:删除根节点之后Merge两颗子树】
- 斜堆的摊还分析
- 将操作后的根节点作为\(D_i\)
- 势能函数的选取:number of heavy nodes
- heavy nodes:if the number of descendants of p's right subtree is at least half of the number of descendants of p, and light otherwise.如果p的右子树的后代数至少是p的后代数的一半,否则为轻。
- The only nodes whose heavy/light status can change are nodes that are initially on the right path
1.4 二项队列
优先队列的一种,是二项树构成的森林
二项树:
\(B_k\)表示高度为k的二项树
一个\(B_k\)的根节点有n个孩子分别为\(B_0,B_1,...B_{n-1}\)
\(B_k\)也可以看作一个\(B_{n-1}\)接到另一个\(B_{n-1}\)的根上构成。
高度为0时元素只有1个
也要满足大小关系,即根最小
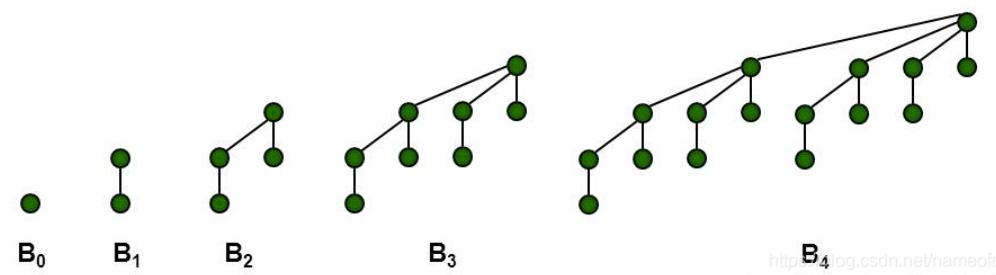
性质:
- 二项树\(B_k\)有\(2^k\)个节点在d深层有\(C_k^d\)个节点
- 在二项队列中每种二项树只能出现一次
- 任意size的二项队列用二项树唯一表示(二进制唯一)
FindMin( )
- 最小值都在二项树的根,因此遍历这个根即可,至多有\(\lceil logN \rceil\)个根,因此\(T_p=O(logN)\)
- 也可以专门维护一个最小值节点
Merge( )
- 类似于二进制加法,有两个阶数一样的二项树就合并为更大的,合并的时候判断根,大的接在小的上面
- \(T=O(logN)\)
Insert( )
- 特殊情况的Merge
- 时间开销最好为O(1),最差为O(logN),即一直需要合并的时候
- 设最小的不存在的Bi,\(T_p=Const(i+1)\)
- \(T_{amorized}=O(1)\)
DeleteMin(H)
- 先找到这个最小值在哪个Bk中 //O(logN)
- 在\(H\)中删除\(B_k\)得到\(H'\) //O(1)
- 将\(B_k\)的根删掉,\(B_k\)变成了\(B_{k-1},...,B_1,B_0\)记为\(H''\) //O(logN)
- 合并\(H',H''\) //O(logN)
【讨论】怎么保证删掉一个根节点后找到它的子树们
答:使用左儿子右兄弟的方法。Root的左边就是儿子儿子的右边就是另外的儿子。
【讨论】使用左儿子右兄弟的方式,子树的高度的排序是怎么样的?
答:从大到小的排序,便于合并,只需要改变根节点的儿子即可保证O(1),从小到大则需要不断扫描。
2. Algorithms
2.1 BackTracking
- 回溯法:相当于枚举所有的可能解,但是这个枚举加上了一定的剪枝
- 缺点:十分复杂,耗时长
2.1.1 Basic Idea
生成解,已经生成了前i个解\((x_1,x_2,...,x_i)\),\(x_k∈S_k(解空间)\)
要添加新元素\(x_{i+1}^{(1)}∈X_{i+1}(第i个解集)\)
检查是否满足要求,若满足要求则生成解\((x_1,x_2,...,x_i,x_{i+1})\)
若不满足则找另一个\(x_{i+1}\),若所有的\(x_{i+1}\)都不满足条件,那么进行回溯
解变为\((x_1,x_2,...,x_{i-1})\)并且标记当前的\(x_i\)为无效解换下一个\(x_i\),以此类推
2.1.2 八皇后问题
【描述】在棋盘中找到八个位置放置皇后,使得它们都不同行且不同列,也不能同时位于对角线上
【Solution】一般使用DFS算法实现。
2.1.3 加油站问题
- 【描述】在一条直线上找到n个地方建立加油站,已知它们两两之间的距离,求出所有加油站的位置,假定第一个加油站的坐标是0
- 【Solution】
- 通过n(n-1)/2个距离算出n
- 0和最大距离说明都都有加油站
- 从D集合中找最大的进行构建,找了就从D中删除距离,失败的话就回到上一种情况.
- 每次检验分成靠左边和靠右边两个情况
1 | bool Reconstruct ( DistType X[ ], DistSet D, int N, int left, int right |
2.1.3 回溯算法的模板
1 | bool Backtracking ( int i ) |
- 回溯选择的方式:应该选择从少到多的回溯方式,可以在剪枝的情况下排除更多的情况
2.1.4 Tic-Tac-Toe
- AI下棋问题:需要推算出所有可能的情况并且选择当前胜率最高的情况往下走
- MinMax Strategy问题:
- 人需要最小化当前情况P的可能赢的情况,而AI要将它最大化
- goodness函数\(f(P)=W_{AI}-W_{Human}\),W是当前情况下某一方可能赢的所有结果,不需要考虑另一方后面会怎么下,只要计算自己在当前局势下的任何可以赢的方法.
2.1.5 剪枝
规则:每次在max里向下取最大的,在min里向下取最小的,并且上面的值是由下一层的取出来得到的,对于不会影响上一层取值的点就可以进行剪枝
α prun
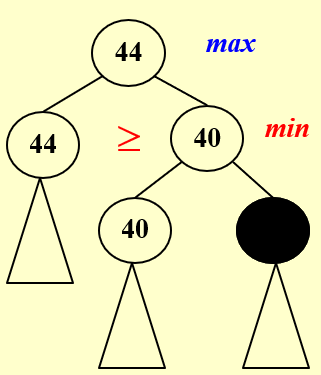 alt="image-20220621203726485" style="zoom:33%;" />
alt="image-20220621203726485" style="zoom:33%;" />β pr
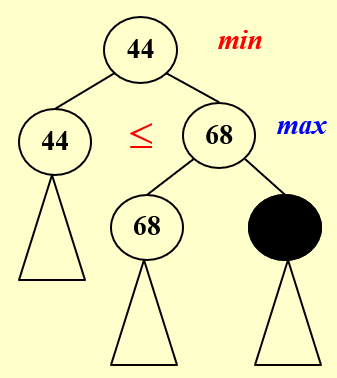 alt="image-20220621203738307" style="zoom:33%;" />
alt="image-20220621203738307" style="zoom:33%;" />
可以把Nsize的game tree限制为搜索\({O(\sqrt N)}\)个节点
1 | What makes the time complexity analysis of a backtracking algorithm very difficult is that the number of solutions that do satisfy the restriction is hard to estimate.(True) |
2.2 Conquer 分治法
Divide:把问题分成几个子问题
Conquer:子问题继续迭代解决
Combine:将子问题的解合并为原本问题的解
能用分治法解决的问题:1. 最大子序列问题(每次分两半,找左右找链接后是否为最大O(NlogN) 2. 树遍历 3. 归并,快排
2.2.1 Closest Points Problem
- 对于N个点,最次的方法就是搜索N(N-1)/2次求出最短距离
- 分治法思路:
- 首先将平面分为两个区域则问题分成三个子问题:右侧最近点对、左侧最近点对、异侧最近点对。
- 要按照x或者y坐标排序后分治
- \(T(N)=3T(N/3)+f(N)\)总的时间复杂度为\(O(NlogN)\)
- 首先将平面分为两个区域则问题分成三个子问题:右侧最近点对、左侧最近点对、异侧最近点对。
2.2.4 基本的迭代
\(T(N)=aT(N/b)+f(N)\)
Substitution Method
- 就是猜加证明
Recursion tree Method
- f(N)就是合并的代价
- 画出树来,底层叶节点个数就是总的真实的计算的花费时间
- 树高与合并有关,树高h则合并h次
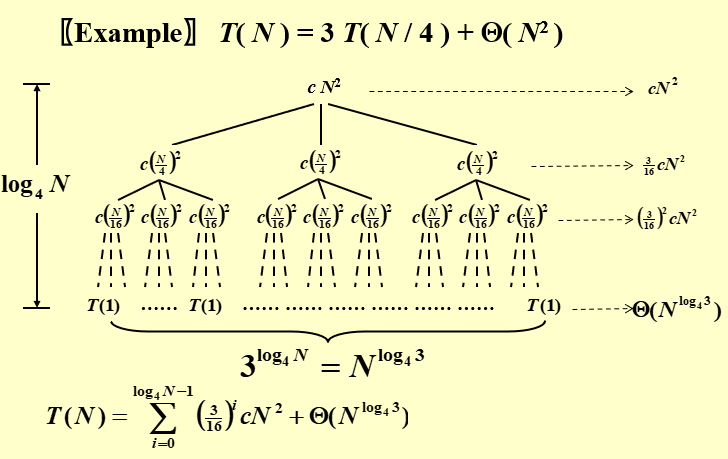 alt="image-20220621212225851" style="zoom:70%;" />
alt="image-20220621212225851" style="zoom:70%;" />
Master Method
- 公式法对于\(T(N)=aT(N/b)+f(N)\)
- \(f(N)=O(N^{log_ba-\epsilon})\)上界则\(T(N)=Θ(N^{log_ba})\)//确界
- \(f(N)=Θ(N^{log_ba})\)确界则\(T(N)=Θ(N^{log_ba}logN)\)
- \(f(N)=Ω(N^{log_ba+\epsilon})\)下界并且\(af(N/b)<cf(N)\)对某个c<1和所有足够大的N成立,则\(T(N)=Θ(f(N))\)
- 总结起来就是三种情况,\(N^{log_ba}\)的渐进上界,等价和渐进下界
- 公式法对于\(T(N)=aT(N/b)+f(N)\)
总结的公式:
- 对于\(T(N)=aT(N/b)+Θ(N^klog^pN)\)
\[ T(N)=\left\{ \begin{matrix} O(N^{log_ba})---------ifa>b^k\\ O(N^k{log^{p+1}N})-------ifa=b^k\\ O(N^k{log^{p}N})--------ifa<b^k\\ \end{matrix} \right. \]
2.3 Dynamic Programming 动态规划
只解决一次子问题,并且适应储存空间记录子问题的结果而不是像递归一样每一次都要重新算。
【例题】Ordering Matrix Multiplications:给出n个矩阵相乘,要找到一种排列方式使得矩阵相乘的开销最小:
传统的算法:计算每一种排列:
- 令\(b_n\)=计算n个矩阵相乘的顺序数.
- \(M_{ij}=M_i·M_{i+1}...·M_j\),则\(b_n=\sum_{i=1}^{n-1}b_ib_{n-i}\)
- \(b_n=O(\frac{4^n}{n\sqrt n})\)
动态规划:
- 设\(m_{ij}\)是计算\(M_i·M_{i+1}...·M_j\)的最小时间开销,那么设\(M_i\)是\(r_{i-1}*r_i\)的尺寸
\[ m_{ij}=\left\{ \begin{matrix} 0-----if\ i=j\\ min_{i≤l<j}\{m_{i,l}+m_{l+1,j}+r_{i-1}r_lr_j\}---if\ j>i \end{matrix} \right. \]
那么动态规划问题中我们要计算的就是\(m_{1,n}\)
【例题】Optimal Binary Search Tree:给出N个words,\(w_i\)与他们的搜索权重\(p_i\),将这些words安排到搜索树上,求最小的搜索时间\(T(N)=\sum_{i=1}^Np_i(1+d_i)\),单个节点深度为0。
答:
- \(T_{ij}=OBST\ of\ w_i,w_{i+1},...,w_j\)
- \(c_{ij}=cost\ of\ T_{ij}\)
- \(r_{ij}=root\ of\ T_{ij}\)
- \(w_{ij}=weight\ of\ T_{ij}=\sum p_k\)
- 由于对于\(T_{ij}\)可以选出一个根节点,那么这个的cost是左树的cost(这里应该是\(w_{ij}\)+\(c_{ij}\))和右树的cost加上搜索根节点的cost
- 则\(c_{ij}=p_k+cost(L)+cost(R)+weight(L)+weight(R)\)
- \(c_{ij}=p_k+c_{i,k-1}+c_{k+1,j}+w_{i,k-1},w_{k+1,j}\)
- \(c_{ij}=w_{ij}+c_{i,k-1}+c_{k+1,j}\)
- \(c_{ij}=min_{i<l≤j}\{w_{ij}+c_{i,k-1}+c_{k+1,j}\}\)
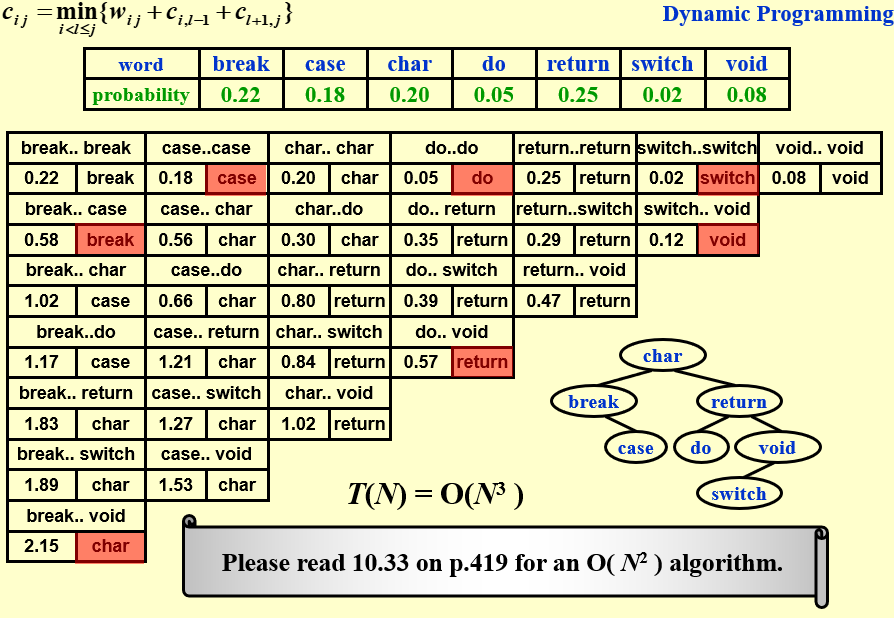
【例题】最短路径问题:所有的\(v_i,v_j\)点对都有一个距离,找出某两点的最短距离
答:
- 【方法一】单源最短路径的dijkstra算法
- 【方法二】动态规划
- 我们设\(D^k[i][j]\)为从i点出发经过前k个点作为中转节点的一部分到达j点的最短路径
- 那我们所求的就是\(D^{N-1}[i][j]\)
- 则首先定义\(D^{-1}[i][j]\)为i直接到j的路径
- 状态转移?
- 从i到j且以k个点为中转的方法:
- i→k点→j,即经过k点
- i→前k-1个点→j,即不经过k点那么可以简化为k-1点为中转站
- 则\(D^k[i][j]=min\{D^{k-1}[i][j],D^{k-1}[i][k]+D^{k-1}[k][j]\}\)

如何设计DP算法?
- 刻画一个最优解【设最优解状态】
- 递归地定义最优值【状态转移方程】
- 按某种顺序计算这些值
- 重构求解策略
【例题】流水线问题,两条流水线之间可以互相传递
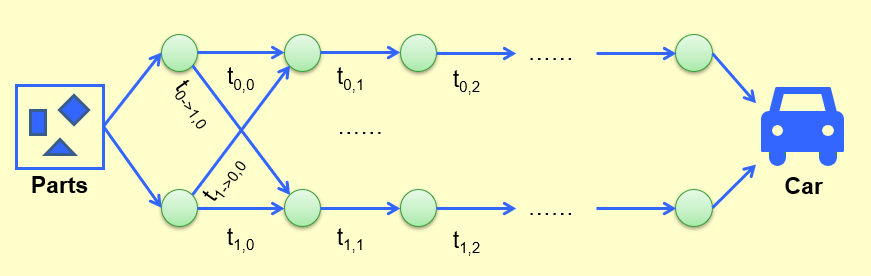
答:
设\(s(t_{i_0},t_{i_1})\)为第i个阶段的上下流水线所需的最小时间
则\(s(t_{\ {i+1}_0},t_{\ {i+1}_1})\)中
- \(t_{\ {i+1}_0}=min\{t_{i_0}+t_{0,i+1},t_{i_1}+t_{1->0,i+1}\}\)
- \(t_{\ {i+1}_1}=min\{t_{i_1}+t_{1,i+1},t_{i_0}+t_{0->1,i+1}\}\)
```cpp f[0][0]=0; L[0][0]=0; f[1][0]=0; L[1][0]=0; for(stage=1; stage<=n; stage++){ for(line=0; line<=1; line++){ f_stay = f[ line][stage-1] + t_process[ line][stage-1]; f_move = f[1-line][stage-1] + t_transit[1-line][stage-1]; if (f_stay<f_move){ f[line][stage] = f_stay; L[line][stage] = line; } else { f[line][stage] = f_move; L[line][stage] = 1-line; } } }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
- 【注意】**若状态之间存在依赖关系,那么不能使用动态规划**
- 【例题】切杆问题:有一根长为L的杆子,有价格表,代表杆子长度从1到L的价格,求最大的收益?
- 答:
- 设长度为n的杆子的最大收益为$R_n$
- 那么对于$R_n$,收益最大有两种情况:单条长度为n最大收益,把n分为了i和n-i把这两种长度的最大收益相加
- $R_n=max\{P_n,max_{1≤i<N}\{R_i+R_{n-i}\}\}$
- 【例题】01背包问题:N个物品重量$w[1],w[2],...,w[n]$,价值为$p[1],p[2],..,p[n]$现有背包最大载重量为W,求最大能够装下多少价值的物品,物品不能切分
- 答:
- 设$dp[i][j]$表示前i件物品装进j载重的背包的最大价值
- 有两种情况:第i件物品装不进来,那么一定是$dp[i][j]=dp[i-1][j]$
- 否则就是装的进来,要比较一下两种情况,一是装进去二是不装进去
- $dp[i][j]=max\{dp[i-1][j],p[i]+dp[i-1][j-w[i]]\}$
### 2.4 Greedy Algorithm 贪心算法
- 定义:每一步做最优的决策即**局部最优**,策略是不变的,决策出来的解直接**作为最终解的一部分**,不进行回溯,但是**不一定是全局最优解**
- 【例题】Activity Select Problem:
- 给出一系列的课$a_1,a_2,..,a_n$,每一个课都有时间($s_i,f_i$)
- 选最大兼容子课
- 贪心:最早开始,时间最短,交点最少(冲突最少)都是错的
- 正确的贪心:最早结束,即让资源尽快free
- Greedy Strategy设计
- 指定贪心策略产生子问题
- 保证贪心选择正确,最优解中有贪心解
- 最优子结构
- 【例题】哈夫曼编码:给出一些字符,我们要对字符产生唯一的编码且要保证可以解码,如a,u,x,z,我们可以分别普通编码为00,01,10,11,为了能够解码,我们需要保证一个字符编码不能成为其他字符编码的前缀。因此我们其实可以使用更加简洁的哈夫曼编码:a=0,u=110,x=10,z=111。给出n个字符,以及他们的出现频率我们要使得编码长度最小,求出哈夫曼编码
- 答:
```cpp
void Huffman ( PriorityQueue heap[ ], int C )
{ consider the C characters as C single node binary trees,
and initialize them into a min heap;
for ( i = 1; i < C; i++ ) {
create a new node;
/* be greedy here */
delete root from min heap and attach it to left_child of node;
delete root from min heap and attach it to right_child of node;
//先用heap选两个频率最小的合成一个节点,节点频率为两个之和
weight of node = sum of weights of its children;
/* weight of a tree = sum of the frequencies of its leaves */
//放回堆里继续选择
insert node into min heap;
}
}
2.5 NP-Completeness NP完全性
- 用于判定一个问题的难/易:说的是yes or no problem
- Euler回路判断问题:所有边访问一遍,那么条件为无向图的所有点度为偶数O(N),属于NP因为能在多项时间内验证解,也是P的能在多项式时间内给出解。
- Hamilton回路问题:包含每一个节点,不存在多项式时间内的解法。
- 单源最短路径无权重:存在多项式时间的解法
- 停机问题:编译器不能发现所有的无限循环
- 图灵机 Turing Machine
- 组成:无限的Memory和扫描头
- scanner 上有若干head,每一个扫描头一次只能指向一个state,并且一次只能左右移动一格
- 可以执行的操作:
- change the finite control state 改变
- erase the symbol in the unit currently pointed by head and write a new symbol in清除并写入
- Head moves on unit to left or right or stays at its current position 左右移动或保持不动
- 确定性图灵机:对于给定的输入每一步的执行都是唯一的
- 不确定性图灵机:对于给定的输入可以自由选择执行的下一步且会选择正确的solution,即能够在多项时间内解决NP问题
- 组成:无限的Memory和扫描头
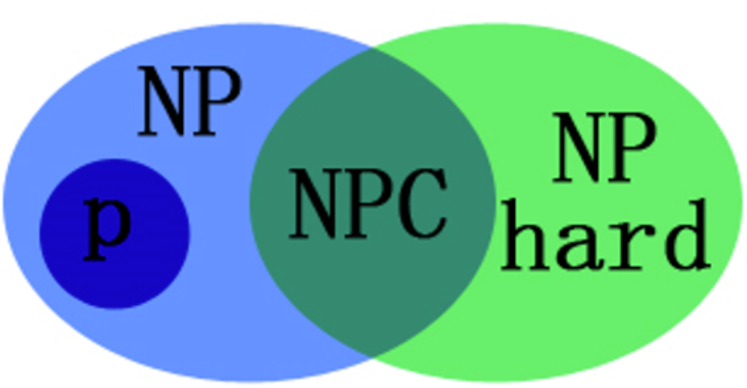
- P problem
- 在多项式时间内可解的问题
- P问题指可以在多项式时间内求解的问题,例如:时间复杂度为O(nlog(n))的快速排序和堆排序,的算法是指数时间算法。
- NP problem
- 不一定在多项式时间内可以给出一个正确解但是给了你一个解之后可以在多项式时间内判断这个解是否正确。
- 如Hamilton回路是NP问题,因为验证一条路是否恰好经过了每一个顶点可在多项式时间内完成,但是找出一个Hamilton回路却要穷举所有可能性,不能直接求解
- 不是所有的decidable problem都是NP问题
- 【P和NP的关系】人类还未解决的问题是:是否所有的NP问题都是P类问题
- \(P\sub NP\)
- 即P问题一定是NP问题
- 【约化/归约/Reduce】
- 概念:如果能找到这样一个变化法则,对任意一个程序A的输入,都能按这个法则变换成程序B的输入,使两程序的输出相同,那么我们说,问题A可约化为问题B,即可以用问题B的解法解决问题A,或者说,问题A可以“变成”问题B。 如:一元一次方程可以“归约”为一元二次方程。这里说的一般是多项式时间内的归约,即把A变成B需要多项式时间,但是B的解决不一定是多项式时间的
- 性质:传递性,A可以约化为B,B可以约化为C,那么C可以约化为A
- 意义:把A归约为B,B的时间复杂度高于或者等于A的时间复杂度。也就是说,问题A不比问题B难。
- 要求:多项式时间内的归约
- NP-Complete Problem
- 一个NPC问题满足以下两个条件:
- 一个NPC问题可以从任何NP问题通过多项式规约得到
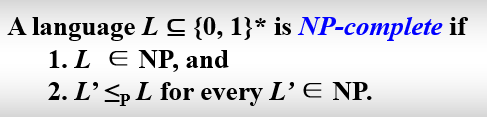
- 问题本身是NP问题
- NPC问题可以互相归约
- 所以显然NP完全问题具有如下性质:它可以在多项式时间内求解,当且仅当所有的其他的NP完全问题也可以在多项式时间内求解。这样一来,只要我们找到一个NPC问题的多项式解,所有的NP问题都可以多项式时间内约化成这个NPC问题,再用多项式时间解决,这样NP就等于P了
- 一个NPC问题满足以下两个条件:
- NP-Hard Problem
- 一个NPH问题满足以下条件:
- 可以由任何NP问题通过多项式归约得到
- 可以不是NP问题,这说明NPH问题的范围比NPC问题更广
- 一个问题是NPC问题那么一定是NPH问题
- 一个NPH问题满足以下条件:
2.6 Approximation 近似算法
- 近似比
- 对于任何规模的n输入,C算法的cost,C*为优化后的cost,那么1≤max{\(\frac{C}{C^{\ *}\ },\frac{C^{\ *}\ }{C}\)}≤ρ(n)
- 如果一个算法的近似率达到了ρ(n)则该算法可以被称为一个ρ(n)-近似算法
- approximation scheme:除了n以外还收一个参数epsilon影响
- PTAS: polynomial-time approximation scheme 关于n成多项式复杂度的算法(对于特定的epsilon)
- FPTAS:fully polynomial-time approximation scheme 关于n和 都成多项式复杂度的算法
【例题】集装箱问题
NextFit:
- 策略:当前箱子放不下就放到新的箱子里去
- 性质:如果最优的方法需要M个箱子那么next fit方法使用的箱子不会超过2M-1,可以用反证法证明,最重要的条件是相邻两个箱子内的和肯定大于1,否则就会放在一个箱子里
FirstFit:
- 策略:从头找箱子,找第一个能放下item的箱子
- 性质:
- 可以用O(NlogN)的时间复杂度来实现这个算法
- 如果最优的方法需要M个箱子那么next fit方法使用的箱子不会超过1.7M
BestFit:
- 策略:找到放下这个物品后剩余空间最小的箱子
- 性质:
- 可以用O(NlogN)的时间复杂度来实现这个算法
- 如果最优的方法需要M个箱子那么next fit方法使用的箱子不会超过1.7M
三种算法都是Online算法,Online算法所需要的箱子数不会少于最优解的5/3倍
OffLine Algorithm
- 在开始装箱之前先检查一次所有的箱子并按照非递增的顺序排序,然后使用First Fit算法,这种情况下需要的箱子的个数不会超过(11M+6)/9 简单的贪心方法会给出一些比较好的结果
【例题】Knapsack Problme 背包问题
- 将N个物品装入容量为M的背包里,每个物品有自己的重量Wi和收益Pi,最终目标是要让收益最大化(近似比2)
- \(p_{max}≤p_{opt}(最优解)≤p_{frac}(物品可以切分的情况)\)
- \(p_{max}≤p_{Greedy}\)
- \(p_{opt}≤p_{frac}=p_{Greedy}+p_{cut}≤p_{Greedy}+p_{max}\)
- \(\frac{p_{opt}\ }{p_{Greedy}\ }≤1+\frac{p_{max}\ }{p_{Greedy}\ }≤2\)
【例题】K-center problem
在给定的N个点的平面中选择K个点(不一定是已有的点)作为中心作圆覆盖所有的点,要求使得这些圆中的最大半径(distance)取得最小值
贪心1:
- 假设所有的center都在点上(将候选集从无穷降下来)
- 设最优解为C,半径为r(C*),那么由于贪心解中心点离其他被覆盖的点距离至多为r,要使得这个r在最优解C*上也正确,则需要r=2r(C*)
- 近似比为2
- O(\(N^2logN\))
```cpp //知道最优解的情况 Centers Greedy-2r ( Sites S[ ], int n, int K, double r ) { Sites S’[ ] = S[ ]; /* S’ is the set of the remaining sites / Centers C[ ] = 空集; while ( S’[ ] != 空集 ) { Select any s from S’ and add it to C; Delete all s’ from S’ that are at dist(s’, s) ≤ 2r; } / end-while */ if ( |C| ≤ K ) return C; else ERROR(No set of K centers with covering radius at most r); }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
- 贪心2:
- 二分法找r,<r<r_{max}$
- O($N^2logN$)
- 每次随机选择点改为中心点,找离这个中心点最远的点si,把si改为中心点
- 近似比为2
- ```cpp
Centers Greedy-Kcenter ( Sites S[ ], int n, int K )
{ Centers C[ ] = 空集;
Select any s from S and add it to C;
while ( |C| < K ) {
Select s from S with maximum dist(s, C);
Add s it to C;
} /* end-while */
return C;
}
除非P=NP,否则没有ρ-近似比解法对任何的ρ成立。

2.7 Local Search 局部搜索
和贪心算法有区别,贪心算法不是局部搜索的特例
局部搜索的框架
Local:局部最优是一个领域内的最佳解决方案
- 邻域Neighborhoods和邻域最优解:设S为目前的解,S~S’记为邻域,S‘为邻域最优的解,邻居是对目前解S的小小的改动
- N(S):为邻域
Search:从邻域的一个点触发找到局部最优解,哪个点?
- Grandient Descent:梯度下降法,找梯度下降最快的方向优化
```cpp SolutionType Gradient_descent() { Start from a feasible solution S ∈ FS ; MinCost = cost(S); while (1) { S’ = Search( N(S) ); /* find the best S’ in N(S) */ CurrentCost = cost(S’); if ( CurrentCost < MinCost ) { MinCost = CurrentCost; S = S’; } //如果邻域内有更好的解则替换 else break; //否则说明当前为最优的 } return S; }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
- 【例题】VCP问题顶点覆盖:给出无向图G=(V,E),找到最小的V的子集S,使得每一条边的至少一个顶点在S中.
- 局部搜索算法1:
1. 先找一个**起点(可行解)**我们选择所有点作为S
2. cost(S)=|S|
3. S~S'邻域:删除一个点成为邻居
4. 这种方法对特殊点有要求(不好)
- 优化方案1:
- 在邻域中随机找S'
- 如果邻居更差那么有几率($e^{-\frac{\Delta cost}{kT}\ }$)使用更差的解替换当前的解
- **可能使用更差的解**
- ```cpp
SolutionType Metropolis()
{ Define constants k and T;
Start from a feasible solution S FS ;
MinCost = cost(S);
while (1) {
S’ = Randomly chosen from N(S);
CurrentCost = cost(S’);
if ( CurrentCost < MinCost ) {
MinCost = CurrentCost; S = S’;
}
else {
With a probability,let S = S’;
else break;
}
}
return S;
}优化方案2:
- 使用模拟退火
- 定义温度T:T越大更多使用乱序,替换概率大
- T在不断下降
【例题】Hopfield Neural Networks
图G=(V,E),每一条边有整数的边权w(正负都有),如果\(w_e<0,e=(u,v)\),则u和v想要有同样的状态(要么都是+1,有么都是-1),如果\(w_e>0\),则u和v想要不同的状态(一个正一个负).
如果\(w_e·s_u·s_v\)<0则说这个边e为好边,否则为坏边
如果一个节点的所有边中:**好边边权和≥坏边边权和*
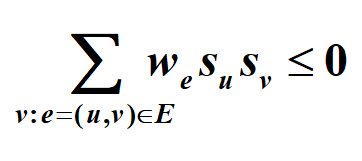 alt="image-20220624092001137" style="zoom:33%;" />
alt="image-20220624092001137" style="zoom:33%;" />当所有的节点都被满足,则记为
稳定态Local Search解法:
- 起点:全部同色
- while(!stable(S))不稳定
- u=GetUnsatisfied(S)将S中的不满足的节点拿出
- \(s_u=-s_u\)
```cpp ConfigType State_flipping() { Start from an arbitrary configuration S; while ( ! IsStable(S) ) { u = GetUnsatisfied(S); su = - su; } return S; }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
- 结论:一定会停下来成为稳定态,最多迭代$\sum_e|w_e|$次
- $\Phi(S)=\sum_{e\ is\ good}|w_e|$
- 设u是不满足的
- $\sum_{e∈(u,v)\&\ e\ is\ bad}|w_e|≥\sum_{e∈(u,v)\&\ e\ is\ good}|w_e|+1$
- 即坏边边权和至少为好边边权和加1
- 将u的颜色反转,会使得跟u有关的e从坏边变好边,好边变坏边.
- $\Phi(S')=\Phi(S)-\sum_{e∈(u',v)\&\ e\ is\ bad}|w_e|+\sum_{e∈(u',v)\&\ e\ is\ good}|w_e|$
- 那么由u为不满足的得知$\Phi(S')≥\Phi(S)+1$
- 这是多项式时间吗?**不是**,因为时间为与W有关的,实际的复杂度与logW有关,是伪多项式的
- 【例题】最大割问题:给一个无向图G=(u,v)每条边都有正边权$w_e$,找一个分割(A,B),使得$w(A,B)=\sum_{\\u∈A,v∈B}w_{uv}$最大
- 转化为Hopfield神经网络
### 2.8 Randomized Algorithm 随机算法
- 用随机的决策处理最坏的情况
- 基本的性质:
- 用非常高的概率给出正确答案
- 总是正确的,并且在期望中运行的很有效率
- 【例子】面试问题:
- 有M个人要雇佣,N个人要进行面试,设面试费用为$C_i$,雇佣费用为$C_h$
- $c_i<<c_h$
- 分析面试cost
- 全部面试再选择人总cost=$O(NC_i+MC_h)$
- solution1:从第一个到最后一个每找到更好的人就雇佣,worst case = O($NC_h$)
- ```cpp
int Hiring ( EventType C[ ], int N )
{ /* candidate 0 is a least-qualified dummy candidate */
int Best = 0;
int BestQ = the quality of candidate 0;
for ( i=1; i<=N; i++ ) {
Qi = interview( i ); /* Ci */
if ( Qi > BestQ ) {
BestQ = Qi;
Best = i;
hire( i ); /* Ch */
}
}
return Best;
}这里的最坏的情况是所有人都是升序的排列,每一个人都要录取
solution2:假设每个人都是随机来的,那么设X为录取数量
- E[X]=\(\sum_{j=1}^Nj·Pr[X=j]\)
- 其中Xi被录取时为1,不被录取为0
- 那么计算每一个人被录取的概率即可算出E[X]
- \(E[x_i]=Pr[i被录取]=\frac{1}{i}\)
- \(E[x]=\sum E[x_i]=lnN\)
- 花费为\(O(C_hlnN+NC_i)\)
solution3:我们直接打乱顺序
```cpp int RandomizedHiring ( EventType C[ ], int N ) { /* candidate 0 is a least-qualified dummy candidate */ int Best = 0; int BestQ = the quality of candidate 0;
randomly permute the list of candidates; for ( i=1; i<=N; i++ ) { Qi = interview( i ); /* Ci */ if ( Qi > BestQ ) { BestQ = Qi; Best = i; hire( i ); /* Ch */ } }1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
- 如何生成随机顺序?
- 对于序列A[i]我们使用P[i]为随机生成的数组,使用P[i]的大小为对应相同i的A[i]排序
- 【例题】在线雇佣问题
- 面试完就要给出结果,只能hire一个人,不能反悔
- 输入序列C[ ],人数N,参数k
- solution:
- 在前k次面试中试出最好的BestQ
- 在从k+1开始面试时,一旦找到比BestQ好的就选择这个人hire,并且break
- ```cpp
int OnlineHiring ( EventType C[ ], int N, int k )
{
int Best = N;
int BestQ = - ;
for ( i=1; i<=k; i++ ) {
Qi = interview( i );
if ( Qi > BestQ ) BestQ = Qi;
}
for ( i=k+1; i<=N; i++ ) {
Qi = interview( i );
if ( Qi > BestQ ) {
Best = i;
break;
}
}
return Best;
}
k的选择?多大概率得到的是最好的?
设\(S\)为第i个是最优的,即i>k,且k+1到i-1之间没有比BestQ更大的
\(P[Best\ one\ in\ i]=\frac{1}{N}\)即i是最好的概率
\(P[No\ one\ hired\ at\ pos\ k+1\ to\ i-1]=\frac{k}{i-1}\)
$Pr[S]={\i=k}^{N-1}={i=k}^{N-1}<img src = "ADS笔记-20220624112801071.png"> alt="image-20220624112801071" style="zoom:40%;" />
则求导知\(k=\frac{N}{e}\)时P最大为\(\frac{1}{e}\)
2.9 Parallel Algorithm 并行算法
硬件并行
并行算法
PRAM模型
WD模
 alt="image-20220624114823335" style="zoom:50%;" />
alt="image-20220624114823335" style="zoom:50%;" />当一个proces
 alt="image-20220624115122011" style="zoom:50%;" />
alt="image-20220624115122011" style="zoom:50%;" />当要
 alt="image-20220624115443182" style="zoom:50%;" />
alt="image-20220624115443182" style="zoom:50%;" />- ```cpp for Pi 1<=i<=n pardo//并行 A(i)=B(i);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
- 可能会产生冲突
- E(Exclusive排他)REW:不可对同一位置进行读写
- C(Concurrent并存的)REW:可以对同一位置读,不可以同时写
- CRCW:可读可写(冲突)
- Arbitrary rule 任意取一个写入
- Priority rule 编号最小的访问写入
- Common rule 写入相同时写入,否则不可写入
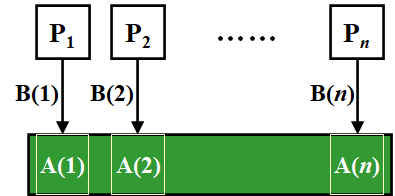
- 【例题】输入A(1),...A(n),计算A(1)+A(2)+...+A(n)
- 处理器读入O(1)
- 二分求和O(logN)
- 第一轮全部的处理器被使用
- 第二轮一半的处理器被使用
- ...
- 最后一轮只有两个被使用后输出总和
- <img src = "ADS笔记\image-20220624131323699.png">
- ```cpp
for Pi,1<=1<n pardo:
B(0,i)=A(i)//并行读入
for h=1 to log_2(n) do
if(i<=n/(2^h))
B(h,i)=B(h-1,2i-1)+B(h-1,2i);
else stay idle//指令idle不做工作但也是指令
//有浪费
for i=1 output B(logn,1) else stay idle
- ```cpp for Pi 1<=i<=n pardo//并行 A(i)=B(i);
WD(Work Depth)模型
```cpp for Pi,1<i<=n pardo: B(0,i):=A(i) for h = 1 to log n for Pi, 1<=i<=n/(2^h) pardo B(h,i) := B(h-1,2i-1) + B(h-1,2i) for i = 1 pardo output B(log n, 1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
- 如何估计一个并行算法?
- Work Load:操作的总次数W(n)
- Worst case running time:T(n)
- 设处理器个数P(n)
- 则$W(n)=P(n)T(n)$
- 实际使用的时间=$\frac{W(n)}{P}$,当$P<\frac{W(n)}{T(n)}$时,时间为$\frac{W(n)}{p}+T(n)$
- 即一个并行算法一定可以在$O(\frac{W(n)}{p}+T(n))$内实现
- 【例题】求上面WD模型解决该问题的Work Load
- WD模型的work load为$n+\frac{n}{2^1}+...+\frac{n}{2^k}=2n$
- WD模型的W(n)=2n,T(n)=2+log n
- 【例题】求前缀和
- 输入A(1),...A(n),计算$\sum_1^1A(i),\sum_1^2A(i),...,\sum_1^nA(i)$
- $C(h,i)=\sum_{\\k=1}^{\alpha}A(k)$,其中α为(0,α)为节点(h,i)的最右节点
- `if(i==1)`:$C(h,i)=B(h,i)$,即**左路径的C(h,i)与B(h,i)相等**
- `if(i%2==0)`:$C(h,i)=C(h+1,i/2)$,即说明的是**同一条右路径的C(h,i)相等**
- `if(i%2==1&&i!=1)`:$C(h,i)=C(h+1,(i-1)/2)+B(h,i)$,找到父亲节点的左兄弟,再加上自己的B(h,i)
- ```cpp
for Pi , 1 ≤ i ≤ n pardo
B(0, i) := A(i) //O(1)
for h = 1 to log n//O(logn)
for i , 1 ≤ i ≤ n/(2^h) pardo//O(1)
B(h, i) := B(h - 1, 2i - 1) + B(h - 1, 2i)
//先算B(h,i)
for h = log n to 0//O(logn)
for i even, 1 ≤ i ≤ n/(2^h) pardo//O(1)
C(h, i) := C(h + 1, i/2)
for i = 1 pardo//O(1)
C(h, 1) := B(h, 1)
for i odd, 3 ≤ i ≤ n/(2^h) pardo//O(1)
C(h, i) := C(h + 1, (i - 1)/2) + B(h, i)
for Pi , 1 ≤ i ≤ n pardo//O(1)
Output C(0, i)- time = T(n) = O(logN)+O(logN)=O(logN)
- work load = W(n)=O (n)+O(n)=O(n)
【例题】数组归并
两个单调不减的数组AB合并为C
化简问题:两个数组的元素个数m=n,且AB中的元素不重复,logn为整数
引入
RANK(j,A)表示B[j]在A中位于第几位,计算A和B的所有RANK,然后用以下方法归并:```cpp for Pi,1≤i≤n pardo: C(i+RANK(i,B)):=A(i) for Pi,1≤j≤n pardo: C(i+RANK(j,A)):=B(i)
1
2
3
4
5
6
7
8
9
10
11
- 只要给出rank函数,我们可以在O(1)时间内和O(n+m)的workload中给出合并
- RANK函数
- 二分搜索:
- ```cpp
for Pi , 1 ≤ i ≤ n pardo:
RANK(i, B) := BS(A(i), B)
RANK(i, A) := BS(B(i), A)T(n)=O(logn)
W(n)=O(nlogn)
Serial Ranking
- ```cpp i = j = 0; while ( i ≤ n || j ≤ m ) { if ( A(i+1) < B(j+1)
) RANK(++i, B) = j; else RANK(++j, A) = i; }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
- T(n)=W(n)=O(n+m)
- Parallel Ranking
- <img src = "ADS笔记\image-20220624143214438.png">
- 步骤一:令$p=\frac{n}{logn}$,把两个数组分别等分成P组,间隔为log n,并计算每个小组中的RANK
- 步骤二:Actual Ranking 有2p个规模为O(log n)的子问题,所以总的时间复杂度还是log n,但是work load变成了O(n)级别
- 【例题】最大值
- 方法一:把求和的+换成max,时间T(n)=O(1),W(n)=$n^2$
- 方法二:分为$\sqrt{n}$组,在每一组里找最大值
- 有$\sqrt n$个组,得到$\sqrt n$个 最大值,耗时T($\sqrt n$),workload为W($\sqrt{n}$)
- $T(n)≤T(\sqrt n)+c_1$
- $W (n)≤\sqrt{n}W(\sqrt{n})+c_2·n$
- $T(n)=O(loglogn),W(n)=O(nloglogn)$
- 方法三:分为$h=loglog\ n$组,在每一组里找最大值
- $T(n)=O(loglogn),W(n)=O(n)$
- 随机算法,高概率$T(n)=O(1),W(n)=O(n)$
- 【Theorem】The algorithm finds the maximum among n elements. With very high probability it runs in O(1) time and O(n) work. The probability of not finishing within this time and work complexity is $O(1/n^c)$for some positive constant c.
- ```cpp
while (there is an element larger than M) {
for (each element larger than M)
Throw it into a random place in a new B(n7/8);
Compute a new M;
}
- ```cpp i = j = 0; while ( i ≤ n || j ≤ m ) { if ( A(i+1) < B(j+1)
) RANK(++i, B) = j; else RANK(++j, A) = i; }
2.10 External Sorting 外部排序
为什么不直接在磁盘上进行快排?
- 磁盘I/O的效率太低了,需要找到磁道和扇区
解决方法:使用tapes进行排序
- tape的特点:只能顺序地访问,不能像内存中的数组一样直接寻址
- 至少需要3条tapes
假如内存里最多可以保持M条记录,对N个元素进行排序
- 每次读出M个数据放进内存进行排序,然后放在tapes中
- 一共需要进行的循环的次数(passes)为1+\(\lceil log_2(N/M) \rceil\)向上取整(2路归并)
【例题】10M组数据,每条128B大小,Memory的大小为4MB,问需要几次pass?
答:passes=\(1+\lceil log_2(1280MB/4MB) \rceil=9\)
优化:减少passes的次数
- 使用k-way的Merge:需要2k个tapes
优化:更少的Tape
- 如何使用3个tapes进行2-way merge?
- 使用不均匀的分割!
- 合并的次数相比于对半分变多了,但是不需要进行磁带的复制,更加节约时间
- 尽量将Run的次数拆分为斐波那契数列,不足的话可以加空的runs.
- 对于k-way的,则为\(F_N^{(k)}=F_{N-1}^{(k)}+F_{N-2}^{(k)}+...+F_{1}^{(k)}\)
- 需要k+1个tapes
- k不是越长越好
- 如何使用3个tapes进行2-way merge?
优化:更长的run
从堆里找root,这个root和下一个进入堆的比较,如果root更小,进来的参与堆排序,否则不参与堆排序即不进入run,把root进入run
直到堆中所有的元素都不能进入run,换一个run
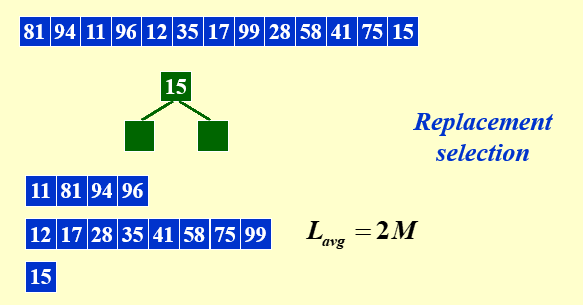
如果内存可以容纳M个元素,则这种方法生成的run的均长度为2M
再输入的元素接近已经排好序的状态时非常work
优化:更小的合并时间:
- 优先合并两个run更小的
- 即长为2,4,5,6的run,先合并2,4变成6,再合并5,6变成11,再合并两个11
使用buffer
- 并行的实际上是对buffer的读和写
- 对于一个k路归并,需要2k个输入buffer和2个输出buffer来进行并行操作
【例题】
Suppose we have the internal memory that can handle 12 numbers at a time, and the following two runs on the tapes:
Run 1: 1, 3, 5, 7, 8, 9, 10, 12
Run 2: 2, 4, 6, 15, 20, 25, 30, 32
Use 2-way merge with 4 input buffers and 2 output buffers for parallel operations. Which of the following three operations are NOT done in parallel?
A.1 and 2 are written onto the third tape; 3 and 4 are merged into an output buffer; 6 and 15 are read into an input buffer
B.3 and 4 are written onto the third tape; 5 and 6 are merged into an output buffer; 8 and 9 are read into an input buffer
C.5 and 6 are written onto the third tape; 7 and 8 are merged into an output buffer; 20 and 25 are read into an input buffer
D.7 and 8 are written onto the third tape; 9 and 15 are merged into an output buffer; 10 and 12 are read into an input buffer
答:D,首先能handle 12个numbers,说明一个buffer有2个number,那么第一轮从两个tape读入一个block

如果您喜欢此博客或发现它对您有用,则欢迎对此发表评论。 也欢迎您共享此博客,以便更多人可以参与。 如果博客中使用的图像侵犯了您的版权,请与作者联系以将其删除。 谢谢 !
