L1
线性变换
- Scale
- \(a(x_a,y_a)\)
- \(b(s_xx_a,s_yy_a)\)
- \(b=Sa\)
- \(S=\begin{bmatrix}s_x\ 0\\0\ s_y\end{bmatrix}\)
- Reflection
- \(b=(-x_a,y_a)\)
- \(S=\begin{bmatrix}-1 \ 0\\0\ 1\end{bmatrix}\)
- Shear
- \(b=(x_a+ay_a,y_a)\)
- \(S=\begin{bmatrix}1 \ a\\0\ 1\end{bmatrix}\)
- 变换矩阵中的(1,0)和(a,1)就是原来的两个标准基的变换后的新标准基
- Rotation
- 逆时针转\(\theta\)度
- 标准基
- (1,0)变为(cos\(\theta\),sin\(\theta\))
- (0,1)变为(-sin\(\theta\),cos\(\theta\))
- 矩阵
- \(S=\begin{bmatrix}cos\theta\ -sin\theta\\sin\theta\ cos\theta\end{bmatrix}\)
- 线性变换
- \(b=Sa\)
- \(\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}a \ b\\c\ d\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}\)
- 平移translate
- \(x'=x+t_x\)
- \(y'=y+t_y\)
- 仿射变换
- \(\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}a \ b\\c\ d\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}+\begin{bmatrix}t_x\\t_y\end{bmatrix}\)
- 想要写成b=Sa的形式
- 升维:
- \(\begin{bmatrix}x'\\y'\\1\end{bmatrix}=\begin{bmatrix}a \ b\ t_x\\c\ d\ t_y\\0\ 0\ 1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}\)
- 反变换
- 逆变换的矩阵是原变换矩阵的逆
- 几何变换不一定有逆变换
L2
小孔相机
- 底片上的每个点会接收到很多点的光,造成模糊,因此需要小孔成像
- 小孔成像下,会有一一对应的关系,孔要足够小
- 这个孔叫
光圈aperture,孔不是越小越好- 进光量
- 衍射效应
- 透镜:
- 焦距:平行光线交汇点\(\frac{1}{f}=\frac{1}{i}+\frac{1}{o}\)
- 物距不变,焦距大,图像远
- 物距不变,焦距小,图像近
- 放大率magnification:\(放大率=\frac{h_i}{h_o}=\frac{i}{o}\)
- 焦距:平行光线交汇点\(\frac{1}{f}=\frac{1}{i}+\frac{1}{o}\)
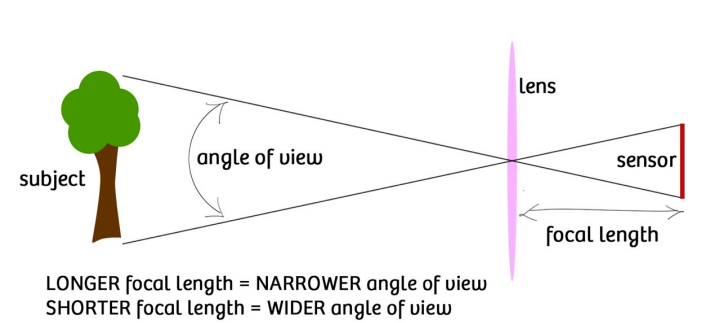
- FOV
- 底片长度有限,只能接收到某个角度内的光线,这个角度就是FOV
- 底片大小固定的情况下,焦距越大,AOV越小;焦距越小,AOV越大。
- 底片长度有限,只能接收到某个角度内的光线,这个角度就是FOV
- 传感器尺寸Sensor size,即底片大小
- 光圈Aperture,透镜的受光面积,由透镜直径表示。
- 光圈的增大缩小影响图像的亮度。
- 影响清晰度,大光圈可以模糊图像
- F-number
- 我们的光圈大小都是和f有关的
- \(D=\frac{f}{N}\)
- 这里的D为光圈直径,f为焦距,N即为F-number
- 我们的光圈大小都是和f有关的
- Lens Defocus
- 像距物距产生偏移,本来一个点在相平面的成像是一个点,结果会成为一个原型的模糊圈。
- \(\frac{b}{D}=\frac{|i'-i|}{i},b=\frac{D}{i}|i'-i|=\frac{f}{iN}|i'-i|\)
- Depth of Field景深
- 产生圆形模糊范围内的物体的最大偏移
- 比如我们产生了直径c的模糊,那么有一个最近的物距和最远的物距,两个差值即为景深
透视变换公式
- 3D世界坐标系到2D图像的坐标系的变换。
- 光轴、相机中心、图像中心
- 在现实中的点\(P=(x,y,z)\)
- 平面上的表示\(p=(u,v)=(f\frac{x}{z},f\frac{y}{z})\)
- 这不是一个线性的变换。为了线性变换,我们写作\((f\frac{x}{z},f\frac{y}{z},1)\)
- 那么齐次坐标下的表达就是\((fx,fy,z)\)
- 那么就可以这么表示:
- \(\begin{bmatrix}f\ 0\ 0\ 0\\0\ f\ 0\ 0\\0\ 0\ 1\ 0\end{bmatrix}\begin{bmatrix}x\\y\\z\\1\end{bmatrix}三维坐标=\begin{bmatrix}fx\\ fy\\ z\end{bmatrix}齐次坐标\approx\begin{bmatrix}f\frac{x}{z}\\f\frac{y}{z}\\1\end{bmatrix}二维坐标\)
- 变换矩阵\(S=\begin{bmatrix}f\ 0\ 0\ 0\\0\ f\ 0\ 0\\0\ 0\ 1\ 0\end{bmatrix}\)
- 损失深度信息
- 性质:保持线性、长度、角度
灭点
- 透视平行线的交点
- 灭点告诉我们线的方向,灭点可能在图像外
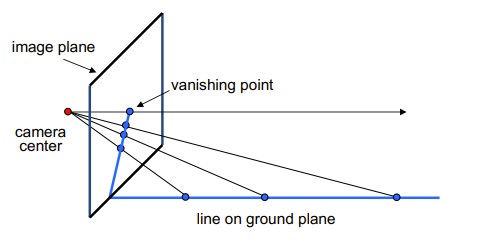
灭线
- 灭点构成的线
- 平面上任意一组平行线定义一个消失点,所有这些消失点的并集就是消失线
- 注意,不同的平面定义不同的消失线
- 消失线的方向告诉我们这个平面的方向
失真Distortion
Perspective Distortion
由于透视近大远小引起的失真

- 外部的柱子显得更大
- 失真不是由于镜头缺陷造成的
Radial Distortion
- 由不完美的镜片引起
- 通过透镜边缘的光线更明显
- Pin cushion,往里面凹
- Barrel,往外面凸
正射投影Orthographic projection
- 透视投影的特殊情况,图像中的点的坐标是实际中的坐标
- 从COP到PP的距离是无限的
- 变换矩阵\(S=\begin{bmatrix}1\ 0\ 0\ 0\\0\ 1\ 0\ 0\\0\ 0\ 0\ 1\end{bmatrix}\)
快门Shutter
- 曝光过程
- 后幕帘开启
- 前幕帘开启,开始曝光
- 后幕帘关闭,曝光结束
- 前幕帘关闭
- 快门速度:控制曝光时间
- 太长:模糊、亮度太大
- 太短:很暗
Rolling Shutter Effect
- 快门一开就开始曝光,每个像素是同时曝光的,Rolling Shutter的开门是一行一行打开的,不是一下子全部打开
- 因此会造成延迟
颜色Color
- 光的波长决定了光的颜色
- RGB:三种颜色
- HSV:颜色离散化,亮度,饱和度
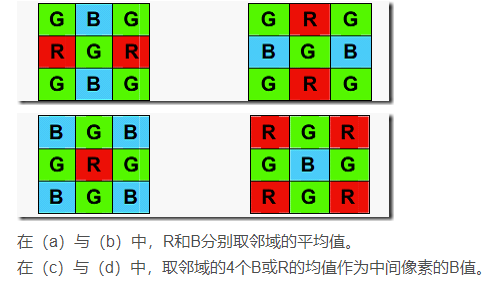
Bayer Filter贝尔滤波器
- 分成若干个2*2的格子,两个记录Green,一个记录Red,一个记录Blue,人对绿色敏感。
- 那么RGB值,就可以由1+2产生,非本单元记录的通道可以使用相邻插值。
L3
图像处理
亮度变化
- 对像素值进行变换,对RGB的值变换
- \(output(x,y)=f(input(x,y))\)
- 曲线S-curve就是暗的更暗,亮的更亮
- 如果是对角线就什么都没变
卷积
- \((f*g)(x)=\int f(y)g(x-y)dy\)
- \(f(y)\)为filter
- \(g(x-y)\)为输入信号
- \((f*g)(x)\)为输出信号
二维卷积
- \((f*g)(x,y)=\sum f(i,j)I(x-i,y-j)\)
- 假设是个2*2的filter,那么ij都只有两个取值
模糊
使用卷积核,如均值模糊、高斯模糊等
- 均值滤波器
- 高斯卷积核
- \(f(i,j)=\frac{1}{2\pi \sigma^2}e^{-\frac{i^2+j^2}{2\sigma^2}}\)
- \(\sigma\)越大越模糊
锐化Sharpen
- \(\begin{bmatrix}0\ -1\ 0\\-1\ 5\ -1\\0\ -1\ 0\end{bmatrix}\)
- sharpening是增大高频成分
- \(I\)为原始图像
- \(I=I-blur(I)\)为高频
- \(I=I+(I-blur(I))\)为sharpen的图像
求梯度,边缘检测
- 左边的减去右边的或者上边的减去下边的
- \(\begin{bmatrix}-1\ 0\ 1\\-2\ 0\ 2\\-1\ 0\ 1\end{bmatrix}\)
- \(\begin{bmatrix}-1\ -2\ -1\\0\ 0\ 0\\1\ 2\ 1\end{bmatrix}\)
双边滤波
- 用途:去除图像的噪声,但是保护边缘
- 高斯滤波器和梯度滤波器的叠加作用
- 在平均时只考虑一侧的平均,变成像\(G\times f\)的滤波器
- 卷积核取决于图像的内容
图像尺寸变换
减小尺寸
- 降采样
- 将连续的变成了离散的,Aliasing
- 摩尔纹、Wagon Wheel illusion
- Aliasing
- 信号改变太快而采样太慢
- 当采样频率慢
- 低频信号:充分采样,合理重构
- 高频信号采样不足:不正确的重构似乎来自低频信号
- 频域:
- 一个信号用傅里叶变换后的函数的频率分布
- 在时域采样就是频域周期延拓[频域采样][https://www.zhihu.com/question/20236413]
- 如何避免aliasing
- 增大采样频率
- Anti-aliasing:采样前过滤掉高频
增大尺寸
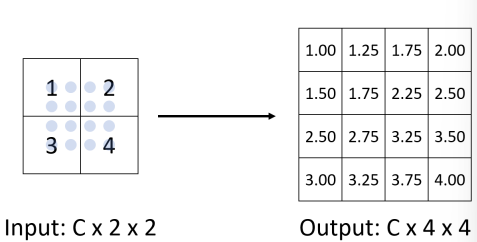
- 上采样
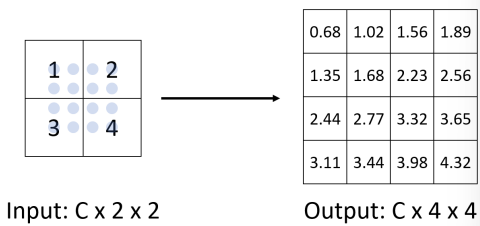
- Bilinear Interpolation
- 取四个最近的点,加权平均,权就是面积
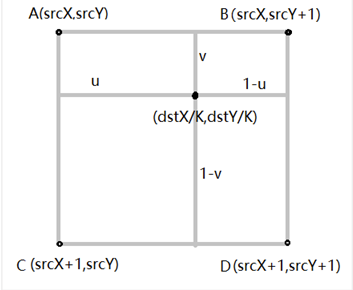
- Bilinear Interpolation
改变图像比例
Seam Caving
- 将不重要的压缩掉,如何自动完成这个操作?
- 裁剪掉梯度变化小的地方
- 衡量像素的重要还是不重要?
- 就是梯度变化
- \(E(I)=|\frac{\partial I}{\partial x}|+|\frac{\partial I}{\partial y}|\)
- 如何实现?
- 卷积,使用edge detect的卷积
- 如何丢掉每一行中的10个像素?
- 希望一条曲线能够穿过一列的要扔掉的像素,找到10条曲线就行。
- 找梯度最小的一条曲线,最短路径问题
L4
优化
梯度下降法
- p:梯度下降方向
- \(\alpha\):步长
- \(x\leftarrow x+\alpha p\)
- 下降方向如何确定:
- 找到下降方向最快的
- 即求导梯度的反方向\(J_F\)
- \(x=x-\alpha J_F(x)\)
- 步长如何确定:
- \(\alpha\)不能太大也不能太小
- 我们需要找到一个最佳的\(\alpha\)
- 使用backtracking
- 初始化\(\alpha\)一个较大的值
- 减小\(\alpha\)直到,\(\phi(\alpha)\leq \phi(0)+\gamma \phi'(0)\alpha\)
- \(\gamma \in (0,1)\)
- 收敛较慢
牛顿法
- \(F(x_k+\Delta x)=F(x_k)+J_F\Delta x+\frac{1}{2}\Delta x^TH_F\Delta x\)
- 找一个使得上式最小的\(\Delta x\)
- \(\Delta x = -H_F^{-1}J_F^T\)
高斯牛顿法
- \(\hat x = argmin_{x}||R(x)||^2_2\)
- 对误差函数进行展开
- 这里\(R(x)=\begin{bmatrix}b_i-f(x_i)\\...\\b_j-f(x_j)\end{bmatrix}\)
- \(||R(x_k+\Delta x)||^2_2=||R(x_k)+J_R\Delta x||^2_2\)
- \(=||R(x_k)||^2_2+2R(x_k)^TJ_R\Delta x+\Delta x^TJ_R^TJ_R\Delta x\)
- \(J_R^TJ_R\Delta x+J_R^TR(x_k)=0\)
- \(J_R\)是R(x)的Jabobian
- \(\Delta x = -(J_R^TJ_R)^{-1}J_R^TR(x_k)\)
- 在牛顿法里我们是\[\Delta x=-H_F^{-1}J_F^{T}=-H_F^{-1}J_F^{T}R(x)\]
- 用了\(J_R\)代替了黑塞矩阵的计算
【Levenberg-Marquardt】求逆会出错,我们可以加一个修正项
- \(\Delta x = -(J_R^TJ_R+\lambda I)^{-1}J_R^TR(x_k)\)
- \(\lambda\)很小
Outlier&Inlier
- Inlier:服从模型假设
- Outlier:与假设有显著差异
RANSAC
Random Sample Concensus随机抽样共识
- 解决outlier的
- 主要思想:
- 内值的分布是相似的,而异常值的分布差异很大
- 使用数据点对进行投票
正则化
为了防止过拟合,正则化的作用:
- 控制参数幅度,不让模型过于复杂
- 限制参数搜索空间
L2
- L2规范化:\(||x||_2=\sum_ix_i^2\)
- L2正则化:
- \(min_x||Ax-b||^2_2\)
- s.t.\(||x||_2\leq 1\)
L1
- L1规范化:\(||x||_1=\sum_i|x_i|\)
- L1正则化:
- \(min_x||Ax-b||^2_2\)
- s.t.\(||x||_1\leq 1\)
L5
特征匹配
步骤
- 特征点检测
- 提取描述符
- 特征点匹配
Harris Operator
- 首先找到H,协方差矩阵
- \(H=\sum_{(u,v)}w(u,v)\begin{bmatrix}I_x^2\ \ I_xI_y\\I_xI_y\ \ I_y^2\end{bmatrix}\)
- \(I_x=\frac{\partial f}{\partial x},I_y=\frac{\partial f}{\partial y}\)
- \(f\)为像素值的函数
- 计算特征值,有两个梯度变化大的,就是角点,那么两个特征值就会变大。
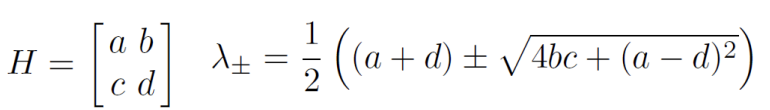
- \(f=\frac{\lambda_1\lambda_2}{\lambda_1+\lambda_2}=\frac{det(H)}{trace(H)}\)
- f是corner response
Harris Detector
- 计算每个像素处的导数
- 在每个像素周围的高斯窗口中计算协方差矩阵H
- 计算角响应函数f
- 阈值f
- 求响应函数的局部极大值(nonmaximum删除)
好的算子需要有好的不变性:
- 光度变换
- 平移
- 旋转
- 缩放
Harris Detector的不变性
- 部分不变到仿射强度变化
- 平移不变性
- 旋转不变性
- 缩放不是不变的
既然对缩放是有改变的,我们如何找到最好的尺度?
- 关键思想:找到给出局部最大值的尺度
Blob Detector
找极值点,即使用\(I_{xx}+I_{yy}\)判断最大最小值,拉普拉斯算子
使用卷积计算\(\nabla ^2=\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}\)
卷积核:
- x方向的:\(\frac{\partial ^2f}{\partial x^2}=f(x+1)+f(x-1)-2f(x)=\begin{bmatrix}1\ -2\ 1\end{bmatrix}\)
- y方向的:\(\frac{\partial ^2f}{\partial y^2}=f(y+1)+f(y-1)-2f(y)=\begin{bmatrix}1\\-2\\1\end{bmatrix}\)
- 复合一下获得拉普拉斯滤波器
- Laplacian Filter
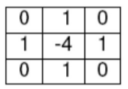
高斯拉普拉斯算子LoG
- 拉普拉斯对噪音很敏感
- 使用LoG
- 先用高斯滤波器平滑图像
- 再用拉普拉斯算子计算
- \(\nabla ^2G=\frac{\partial ^2G}{\partial x^2}+\frac{\partial ^2G}{\partial y^2}\)
- scale of LoG被高斯的\(\sigma\)控制
- 因此我们用不同的σ去做卷积获得不同大小的blob
高斯差值DoG
对拉普拉斯高斯的近似,LoG能被两个高斯的差值近似,即\(\nabla ^2G_{\sigma}=G_{\sigma_1}-G_{\sigma_2}\)
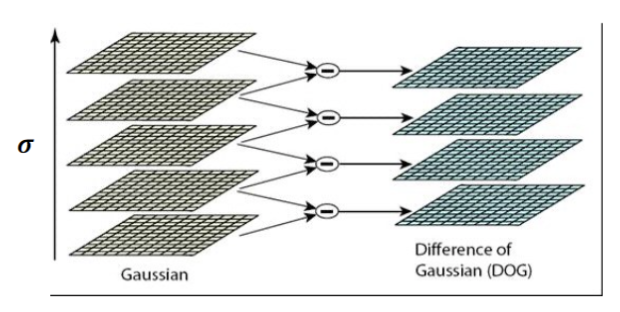
- 计算高效,一般使用这个来计算
SIFT
如何描述特征?
- 每一个像素有一个梯度,梯度有一个朝向
- 把所有像素的梯度放在一起,有一个梯度方向的直方图
- 用这个直方图作为描述子,就是区域内梯度朝向的分布
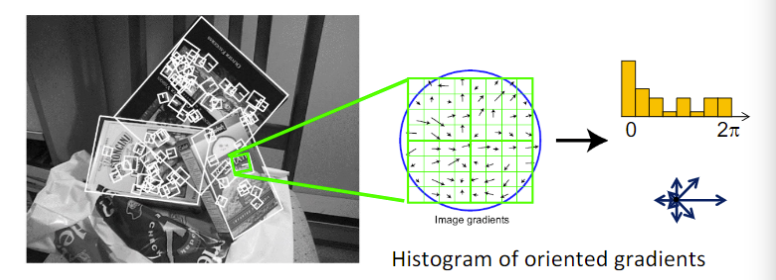
不变性?
- 强度变化:有不变性,只需要方向,不需要大小
- 旋转变化:没有不变性,直方图平移,normalize一下就可以了
- 构造descriptor时,让主朝向在第一位
- 缩放变化:没有不变性,在detection的阶段就处理了,在detection阶段的scale确定了就要处理
Matching
如何进行匹配?
定义两个描述符的距离,算一个相似度,取最相似的,相似度的衡量,计算两个descriptor的距离,距离小,相似。对于图1的一个特征点,从图2中找到距离最小的描述符对应的特征点。
但是如果有重复的纹理,就不一定有唯一解了,如何解决?
Ratio test
- \(Ratio\ score =||f_1-f_2||/||f_1-f_2'||\)
- f2为最相似的,f2‘为第二相似的,那么ratio score接近于1,说明是没有奇异性的,那么我们就不要这个点了。
Mutual nearest neighbor
另一种策略:找到相互最近的邻居
f2是l2中f1的最近邻居
f1是l1中f2最近的邻居
Motion Estimation
- Feature-tracking
- 我们需要跟踪每一个特征点在视频每一帧的位置
- 侧重在视频中,时序关系
- output:displacement of sparse points稀疏点的位移
- Optical flow
- 我们希望恢复图像中每一个像素的运动
- output:dense displacement field密集位移场
Lucas-Kanade Method
假设图像中有特征点,从时刻t到时刻t+1,通过运动估计得到时刻t+1的点的位置,查看我们预测的位置和真实位置的误差。
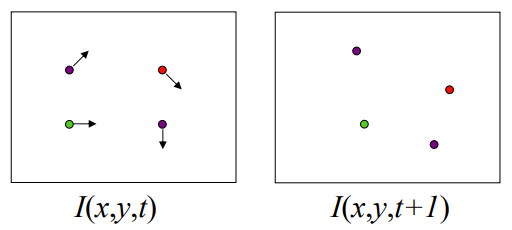
就是求每一个点对应的平移向量。
- 我们可以用feature mapping做,但是时序上的特征无法很好的体现。
- Lucas-Kanade方法的假设
- 小位移:点的位置变化不会太大
- 亮度恒常性:前后帧对应点的亮度值不会太大变化。
- 空间相干性:空间上的连续性,相邻的点运动比较一致
Brightness Constancy Equation:
- \(I(x,y,t)=I(x+u,y+v,t+1)\)
- 我们要求解的就是u和v
- $I $是我们的图像,是没有表达式的
Small Motion:
- 使用泰勒展开:
- \(I(x+u,y+v,t+1)=I(x,y,z)+I_xu+I_yv+I_t\)
- \(I_x,I_y\)就是关于图像的导数,使用卷积可以求
- \(I_t\)是关于时间的导数,就是第一张图的xy上的像素值减去第二张图同样位置的xy的像素值
- 那么我们就得到了
- \(I_xu+I_yv+I_t=0\)
- \(\nabla I[u\ v]^T+I_t=0\)
- 只有一个方程无法计算u和v
Spatial coherence
- 相邻的点我们可以假设u和v是一样的
- 那么我们的方程就变多了
\(\nabla I[u\ v]^T+I_t=0\)
我们现在一个方程,两个未知数(u,v),假设我们的u,v满足以上的方程,如果
\(\nabla I[u'\ v']^T=0\)
那么(u+u',v+v')也满足这个方程。
孔径问题
对一个点而言,垂直于图像梯度方向的移动无法确定。孔径问题。
假设我们使用5*5的窗口,那么我们就有25个方程。
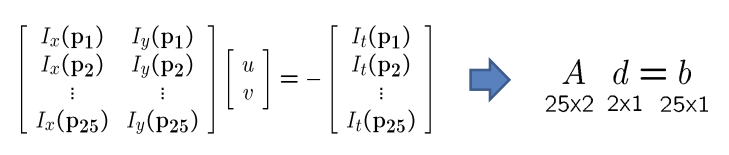
两个变量25个方程如何解决?我们找一组u,v使得误差最小,即优化问题。
\(min_{d}||Ad-b||^2\)
求导,找零点。\((A^TA)d=A^Tb\)
那么有:
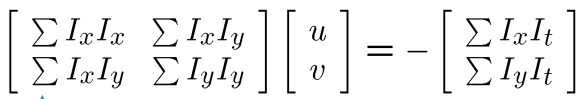
那么想要有唯一解,有要求\((A^TA)\)满秩,保证其可逆,有两个不为0的特征值。
有稳定的解时,\((A^TA)\)的两个特征值要比较大
这个与corner detector比较类似。换言之,角点的optimal flow更容易追踪。
L6
图像的拼接
将一张图进行变换,与另一张图重合。改变图像的形状,不改变强度。
Global Warping:对所有点改变位置的规律是一致的。
Parametric Warping:变换可以用参数表示。
\(p'=T(p)\)
- Scale缩放
- Reflection反转
- Shear剪切
- Rotation旋转
- Tanslation可以用升维的方式,齐次坐标
仿射变换(线性变换+平移)的最后一行要是[0 0 1],如果不是呢?
仿射变换的自由度为6
投影变换(单应性),投影变换的最后一行可以不是[0 0 1],但是我们约束了变换矩阵的模为1,因此投影变换的自由度为8
- 平移自由度2
- 欧式变换平移+旋转自由度2+1
- 相似变换平移+旋转+缩放2+1+1
- 仿射自由度6
- 投影自由度8
图像的缝合
通过matching获得对应点,计算变换矩阵T
\(\begin{bmatrix}x'\\y'\\1\end{bmatrix}=T\begin{bmatrix}x\\y\\1\end{bmatrix}\)
- 对于仿射变换,我们有6个自由度,我们需要3对匹配点来解
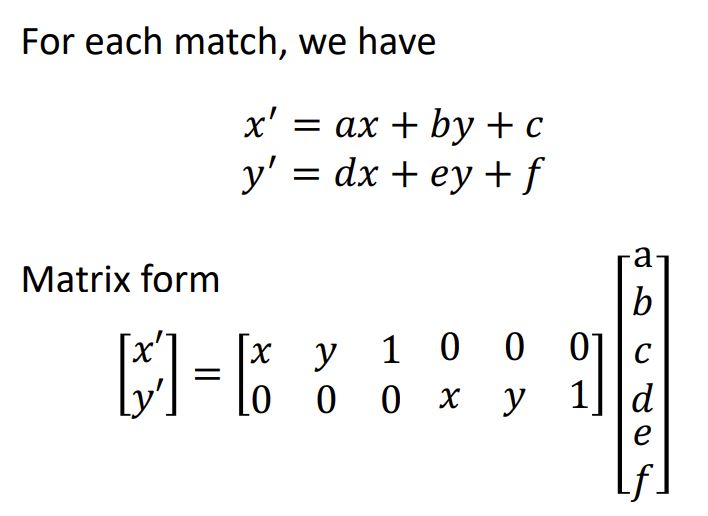
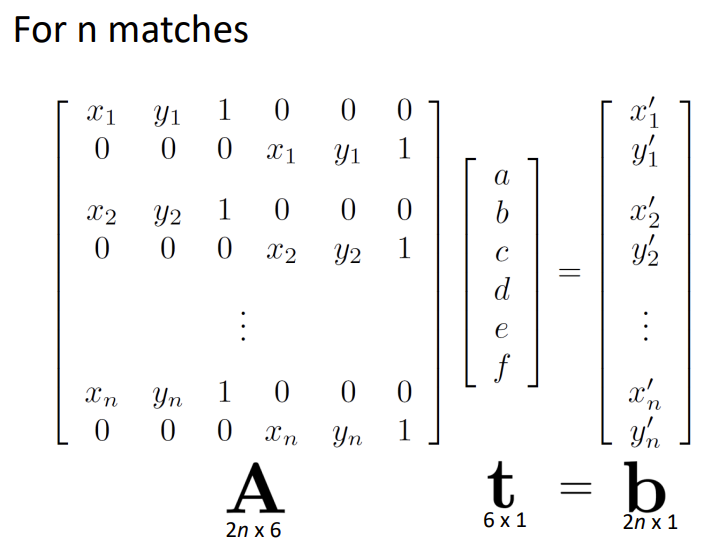
对于n对点的情况下,我么使用最小二乘法,优化问题求解
\(t=(A^TA)^{-1}A^Tb\)
对于投影变换,我们有9个未知数,当然可以用模长限制为8个未知数。
我们需要至少4对点来求解。
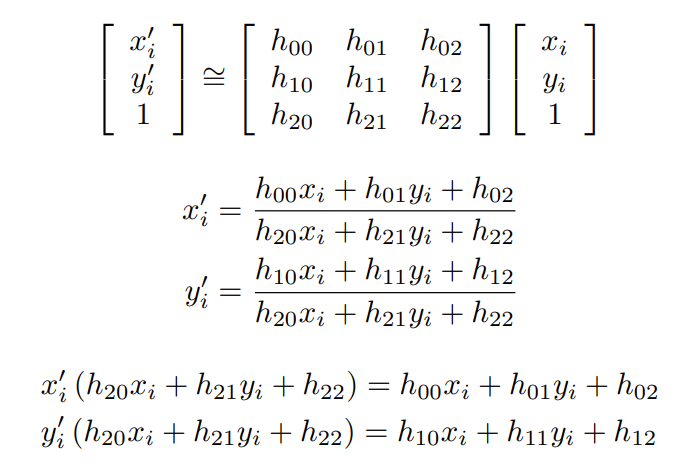
这里的分母是1,使用齐次化的方法。
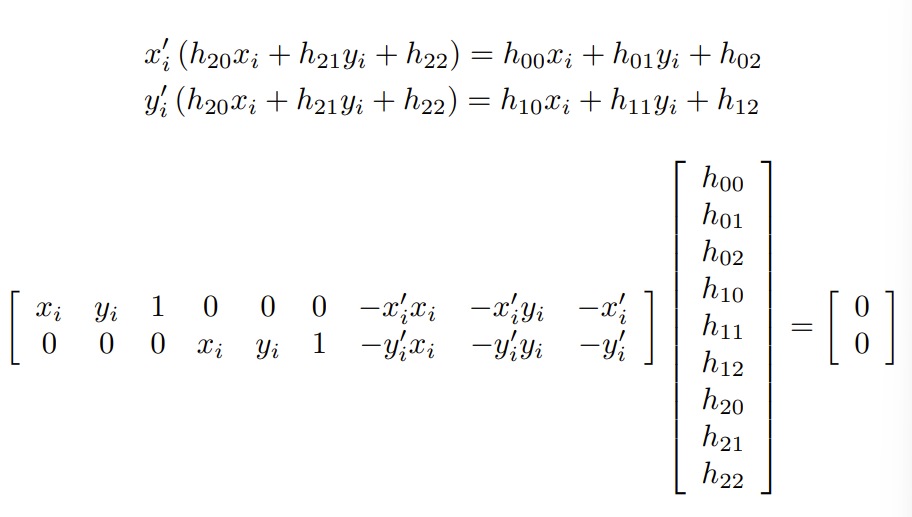

RANSAC
- Randomly choose s samples随机选s个sample
- Typically s = minimum sample size that lets you fit a model
- Fit a model (e.g., transformation matrix) to those samples
- fit一个模型
- Count the number of inliers that approximately fit the model
- 计算inlier数量
- Repeat N times
- 重复N次
- Choose the model that has the largest set of inliers
- 挑选最多inliner的model
- Randomly choose s samples随机选s个sample
L7
Structure From Motion
Camera Model
- 相机摆在一个位置pose
- 将现实的坐标点进行几何变换,到相机坐标中
- 坐标系转换,从世界坐标系到相机坐标系:外参矩阵
- 透视投影,图像平面图像传感器的映射:内参矩阵
坐标转换
从世界坐标系到相机坐标系的旋转矩阵为R,相机位置为\(C_w\)

那么变换为\(X_c=R(X_w-C_w)\)
\(X_c=RX_w+t,t=-RC_w\)
我们同样可以用一个4×4的矩阵表示,就是外参矩阵\(M_{ext}\)

透视投影
相机坐标系的三维坐标要转换成像平面的二维坐标
\(x_c=\begin{bmatrix}x_c\\y_c\\z_c\end{bmatrix}\)
\(x_i=f\begin{bmatrix}x_c/z_c\\y_c/z_c\\1\end{bmatrix}\)
像平面到传感器的映射
到上面那一步的单位还是mm,我们需要的是pixel。
假设我们的分辨率为\(m_x,m_y\)
\(u=m_xf\frac{x_c}{z_c}+c_x\)
\(v=m_yf\frac{y_c}{z_c}+c_y\)
那么在齐次坐标系下:
\(\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}f_x\ 0\ c_x\\0\ f_y\ c_y\\0\ 0\ 1\end{bmatrix}\begin{bmatrix}x_c\\y_c\\z_c\end{bmatrix}=\begin{bmatrix}f_x\ 0\ c_x\ 0\\0\ f_y\ c_y\ 0\\0\ 0\ 1\ 0\end{bmatrix}\begin{bmatrix}x_c\\y_c\\z_c\\1\end{bmatrix}\)
\(f_x=m_xf\)
\(f_y=m_yf\)
这个就是相机的内参矩阵3×4\(M_{int}\)
投影矩阵
\(u=M_{int}M_{ext}x_w\)
我们记内参矩阵×外参矩阵为投影矩阵P
相机标定
给我一张图像,如何找这个内参矩阵和外参矩阵的参数呢?如何在世界坐标系下计算相机的位置和方向?相机标定。
捕获具有已知几何形状的物体的图像,例如校准板,得到一些角点的世界坐标
对其进行拍照,通过角点检测匹配,知道三维点对应的二维坐标
对于场景和图像中的每个对应点,带入计算投影矩阵的参数

解优化问题
像前面的图像缝合的一样的方法,我们进行约束

\(||p||^2=1\)
求解\(Ap=0\)
即\(min_p||Ap||^2\)
可以证明矩阵\(A^TA\)的特征向量\(p\)具有最小的特征值\(λ\)是解。
我们获得了P的参数就获得了P矩阵,接下来我们要求\(M_{int},M_{ext}\)
我们对P矩阵左边的3×3的矩阵使用QR分解获得上三角阵K和一个正交矩阵R。
那么我们知道K就是内参矩阵的左边3×3的,R是我们的旋转矩阵,我们还需要一个平移参数t。
根据公式我们知道\(t=K^{-1}\begin{bmatrix}p_{14}\\p_{24}\\p_{34}\end{bmatrix}\)
PnP问题
求解世界坐标系和相机坐标系的位置关系,给定3D-2D对应
我们有6个未知数:旋转3个,平移3个
也是6DoF,6自由度位置位置问题
最少三对点,但是三对点不够!
位姿估计
类似于视觉定位,获得物体在相机坐标系下的旋转和平移是怎么样的
SfM
- 假设每个相机的内在矩阵K都是已知的
- 找到几个可靠的对应点
- 求出相对相机位置t和方向R
- 寻找场景点的三维位置
特征匹配:获得匹配的特征点对
通过对应关系,求解两个相机的相对位置
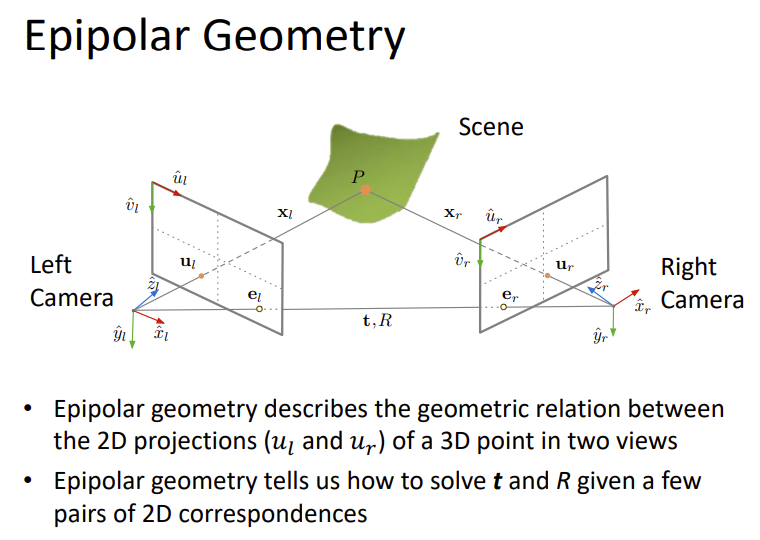
- 极线:极平面和像平面的交线
- 极点:相机连线和像平面的交点,即相机在另一个相机中成像的点
- P点的极平面:点P和相机位置形成的平面
- 极线约束:
- 极平面的法向量:\(n=t\times x_l\),t是两个相机的位移,\(x_l\)是P点到左边相机的的向量
- \(x_l·(t\times x_l)=0\)

- 将左边的l坐标替换为r的
- \(E=T_{×}R\)
- \(x_l^TEx_r=0\)
- 当我们知道了E,我们可以通过奇异值分解获得\(T_×\)和\(R\),即可以获得t和R
如何获得E?
我们的\(x_l,x_r\)都是三维坐标,如果我们只有二维坐标呢?
\(z_l\begin{bmatrix}u_l\\v_l\\1\end{bmatrix}=\begin{bmatrix}z_lu_l\\z_lv_l\\z_l\end{bmatrix}=\begin{bmatrix}f_x^l\ 0\ o_x^l\\0f_y^l\ o_y^l\\ 0\ 0\ 1\end{bmatrix}\begin{bmatrix}x_l\\y_l\\z_l\end{bmatrix}=K_l\begin{bmatrix}x_l\\y_l\\z_l\end{bmatrix}\)
\(z_r\begin{bmatrix}u_r\\v_r\\1\end{bmatrix}=\begin{bmatrix}z_ru_r\\z_rv_r\\z_r\end{bmatrix}=\begin{bmatrix}f_x^r\ 0\ o_x^r\\0f_y^r\ o_y^r\\ 0\ 0\ 1\end{bmatrix}\begin{bmatrix}x_r\\y_r\\z_r\end{bmatrix}=K_r\begin{bmatrix}x_r\\y_r\\z_r\end{bmatrix}\)
那么极线约束就变成了
\([u_l\ v_l\ 1]{K_l^{-1}}^TEK_r^{-1}\begin{bmatrix}u_r\\v_r\\1\end{bmatrix}=0\)
\(F={K_l^{-1}}^TEK_r^{-1}\)
\([u_l\ v_l\ 1]F\begin{bmatrix}u_r\\v_r\\1\end{bmatrix}=0\)
\(E=K_l^TFK_r\)
这里的F可以替换为kF,增加一个任意的缩放,这里我们可以添加限制为\(||f||^2=1\)
相对相机姿态估计
- 对于每个对应i,写出外极约束。
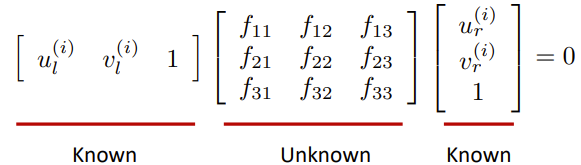
- 重新排列项以形成线性系统。

- 求基本矩阵F的最小二乘解。我们想让Af尽可能接近0,且\(||f||^2=1\)
- 解出了F,我们计算E,\(E=K_l^TFK_r\)
- 从E中解出R和t,奇异值分解
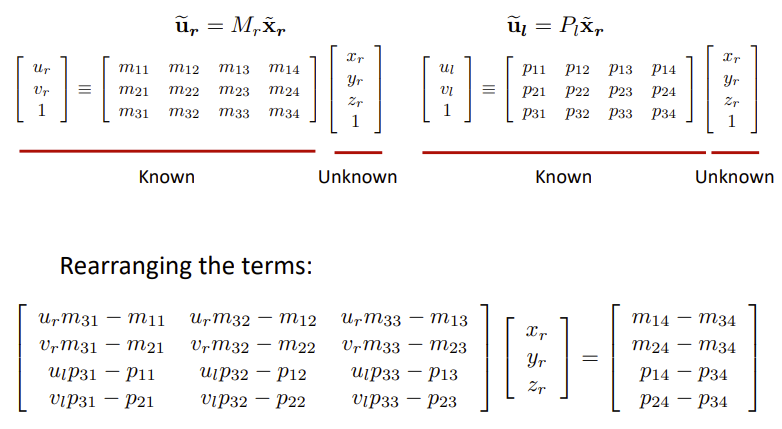
Triangulation
给定相应的二维特征点和摄像机参数,如何找到场景点的三维坐标?
给定了二维特征点和相机内参,我么可以计算出三维点。
\(\hat u_l=M_{int}^l\hat x_l\)
\(\hat u_r=M_{int}^r\hat x_r\)
\(\hat x_l=M_{ext}^l\hat x_r\)
我们有
\(\hat u_l=P_l \hat x_r\)
\(\hat u_r = M_{int}^r\hat x_r\)

Sequential Structure from Motion
- 初始化相机运动和场景结构
- 对于每个额外的视图
- 利用新相机图像中所有可见的已知三维点,确定新相机的投影矩阵
- 优化和扩展结构:计算新的3D点,重新优化现有的点,也被这台相机看到
- 细化结构和运动:束调整
L8
深度感知
- 主动:雷达传感器、结构光、active stereo立体视觉
- 被动:Structure From Motion、stereo立体视觉
Stereo Vision
两只眼睛看一个东西,使用视差,从而感知距离。
假设相机相对位置已经固定,如何估计所有点的深度?
给定了\(X_L\),\(X_R\)一定在极线上!具体位置和\(X_L\)对应的具体深度有关
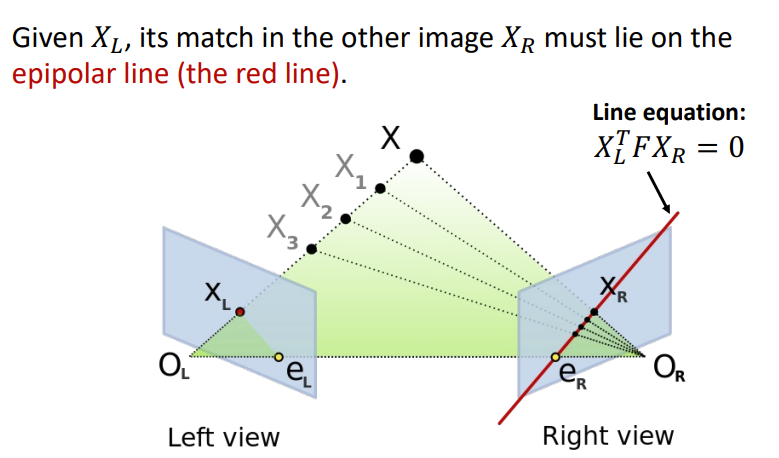
我们搜索匹配点时,只需要沿着极线寻找即可。
当两个相机水平,极线就是水平的,最好寻找!
Depth from disparity
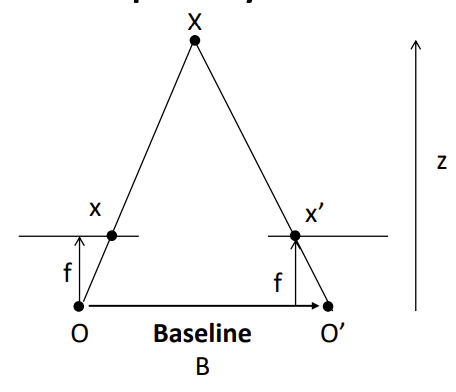
视差,就是两个极点之间的距离,即\(x_2-x_1\)
\(disparity=x-x'=\frac{Bf}{z}\)
这里的B是两个相机的距离,即Baseline,f为焦距,z为深度
- B小:深度误差大
- B大:困难的搜索问题
当epipolar line不是水平的时候怎么办?
图像矫正,实际的相平面不是满足水平的。我们假设我们调整了相机获得了水平线的虚相机平面,原平面和虚平面有一一对应关系。使用几何变换。
匹配:我们的匹配是在及线上进行搜索,然后计算不相似度(距离),选择距离最小的就是匹配
Stereo reconstruction pipeline
- 校准相机
- 纠正图像
- 计算视差
- 估计深度
误差:存在相机标定的误差、图像分辨率差、遮挡误差、违反亮度恒定误差、纹理稀少存在误差
Multi-view Stereo
优点
- 可以匹配窗口使用超过1个邻居,给一个更强的约束
- 如果你有很多潜在的邻居,可以选择邻居的最佳子集来匹配每个参考图像
- 能否为每个参考帧重建一个深度图,并合并成一个完整的3D模型
对每一个视角,我们取其周围的视角的一起计算深度图,每一个视角都会有一个深度图
计算每个点的深度时,我们尝试不同深度与周围视角的误差,取最小的误差的深度。
对于一个ref view,我们想知道其深度,那么我们就尝试一个深度,将这个深度代入到neighbor view中进行计算误差,寻找误差最小的深度。
Plane-Sweep
对于一个像素的深度为d,那么我们投影到其他的邻居相机中计算误差,这个过程可以直接在平面上进行,更高效计算。就是说我们对所有的像素尝试一个深度,进行计算误差。
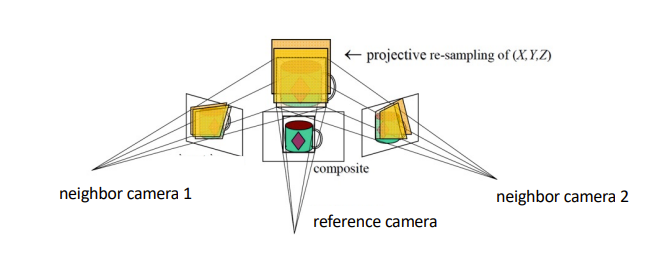
- 平行于参考相机图像平面的扫描平面族
- 将每个平面投影到相邻视图(通过单应性)并比较像素值
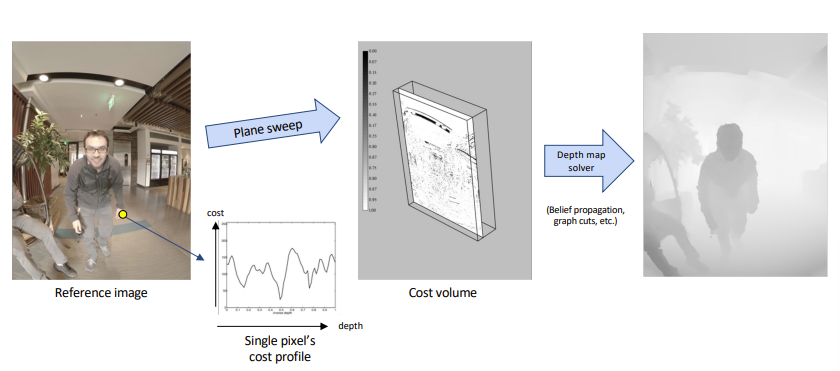
最后得到了Cost Volumes,是一个3D数组,它存储所有像素在所有深度的误差。类似于穷举。
3D Representations
- 点云:一系列3D点
- +容易获取
- -空间开销大
- -缺少点与点之间连接关系
- 体素:Occupancy、Signed Distance(SDF)
- Voxel
- 三维的离散化的格子
- voxel,立方体的值代表这个点是否被占用。
- +规则表示,容易送入网络学习
- +可以处理任意拓扑结构
- -随着分辨率增加,内存呈立方级增长
- -物体表示不够精细
- -纹理不友好
- SDF:点到形状边界的距离,距离由一个度规定义,通常是欧几里得距离
- +可以精细建模细节,理论上分辨率无穷
- +内存占用少
- +网络易于学习
- -需后处理得到显式几何结构
- Voxel
- Mesh:网格
- 通常是三角网格
- +高质量描述 3D 几何结构
- +内存占有较少
- +纹理友好
- -网络难以学习
- -不同物体类别需要不同的mesh模板
- Occupancy Function
- 使用一个函数划分一个边界面
- +可以精细建模细节,理论上分辨率无穷
- +内存占用少
- +网络易于学习
- -需后处理得到显式几何结构
重建方法
- 深度图转化为体素
- KinectFusion,
- Poisson reconstruction
泊松重建
输入点云,输出体素
Marching cubes
从Volume提取Mesh
1 | MC算法实际上是一个分而治之的方法,因为其将等值面的抽取分布于每一个体素(voxel)中进行。对于每个被处理的体素,以三角面片来逼近其内部的等值面。每个体素是一个小立方体(cube),在构造三角面片的处理过程中对每个体素都“扫描”一遍,就好像是一个处理器在这些体素上移动一样,也因此而得名。 |
L9
线性分类器
- 输入:image
- 输出:类别的得分
数据驱动,我们输入一系列的数据集(图像和标签),训练一个分类器,用以分类新的图像
\(f(x,W)\),x为图像,W为参数
\(f(x,W)=Wx+b\)
Loss Function
MSE loss:\(min_w\sum_i(y_i-f_w(x_i))^2\)
能用MSEloss给分类任务吗?不能,标签是离散的,分数是实数
类标签可以看作概率
- 将分数转换为概率
- softmax:\(\sigma(z)_j=\frac{e^{z_j}}{\sum_k e^{z_k}}\)
- 计算预测和真实概率之间的交叉熵
- \(-\sum c_i\ log(p_i)\)
- ci为类别,pi为该类别的概率
神经网络
一般的全连接的神经网络是线性的(感知机),如何变成非线性的?
- \(f(x,W)=Wx+b\)
- \(f(x,W)=\sigma(Wx+b)\)
- 增加一个激活函数Relu、sigmoid等
多层感知机
可以写成函数表达式,比如有一个隐藏层的多层感知机
\(f(x)=\sigma (W_2(\sigma(W_1x+b_1))+b_2)\)
卷积神经网络
我们可以通过局部模式来识别图像,我们使用卷积来实现类似的识别
基本模式:卷积、非线性化(激活)、池化
二维卷积
图像大小:image size
卷积核大小:Filter size
- 输出feature map大小:image size-Filter size+1
- 有Padding和stride的情况:(image size-Filter size+Padding*2)/Stride
如果有通道,那么我们的卷积核也要是对应通道数的
Pooling
- Max Pooling:将区域内的值合并后设置为最大值
- Average Pooling::区域内的值合并后全部是平均值
为什么用卷积神经网络
卷积神经网络能够用卷积的方式从原信息中提取"部分特定的信息(信息跟卷积核相关)",且对于二维的图像来说是原生支持的(不需要处理),这就保留了图像中的空间信息,而空间信息是具有可平移性质的
神经网络的训练
梯度下降法训练神经网络
- 设定参数
- 计算损失函数
- 进行梯度下降:backpropagation
- 通过网络转发数据,得到丢失
- Backprop计算梯度
- 使用渐变更新参数
- 如果未融合,请执行步骤1
Data
数据的分割,我们的数据集可以分为train、test和validation
只分为train和test的话,我们不知道它在新数据上的表现
Data augmentation
数据增强,我们可以将同一个训练图像进行几何变换等方式产生新的屯连图像,从而扩大我们的数据集。
过拟合
参数过于复杂的情况,我们可以添加Cross validation、早停、正则化项、Dropout、数据增强等来避免。
L10
语义分割
用类别标签标记图像中的每个像素不要区分实例,将每一个像素给一个分类的标签
- 效率很低,并且全局信息较少。
Sliding window,我们使用滑动的窗口,用CNN来判定窗口中心的分类
全卷积神经网络
- 一次性做出预测
- 训练的损失函数是什么?逐像素交叉熵
该网络在前面两步跟CNN的结构是一样的,但是在CNN网络Flatten的时候,FCN网络将之换成了一个卷积核size为5x5,输出通道为50的卷积层,之后的全连接层都换成了1x1的卷积层。
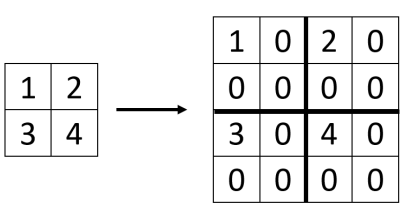
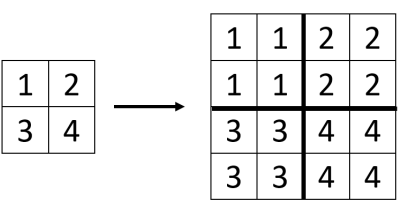
Unpooling
- Bed of Nails
- Nearest Neighbor
- Bilinear Interpolation
- Bicubic Interpolation
Object detection
输入:一张RGB图像
输出:一些bounding box,包裹检测的物体
Detecting a single object
一张图像,输入到全连接神经网络中输出1000个分类的概率预测
同时输入到一个输出4维度的box坐标、
这样我们获得了物体的label以及bounding box的位置
Detecting multiple objects
每张图像需要不同数量的输出
将CNN应用于图像的许多不同作物,CNN将每个作物分类为对象或背景
假设box的大小为h*w
- x的可能位置W-w+1
- y的可能位置H-h+1
- bbox的所有可能位置(W-w+1)*(H-h+1)
显然这样子太难算了
Region proposals
- 找到一组可能涵盖所有对象的小盒子
- 通常是基于启发式的
- 通过过分割
- 跑得相对快:选择性搜索在CPU上几秒钟内提供2000个区域建议
R-CNN
对于我们可能区域,进行计算,把每一个区域进行resize到224*224,输入到CNN
进行class scores和bbox的预测
使用分数选择要输出的区域建议的子集
评价指标
IoU:
- \(IoU=\frac{Area\ of Intersection}{Area\ of\ Union}\)
- IoU越大说明和真实的越接近,越好
Fast R-CNN
1 | Fast RCNN与RCNN的不同主要在于Fast RCNN引入了ROI Pooling,在RCNN中,在进行卷积操作之前一般都是先将图片分割与形变到固定尺寸,这也正是RCNN的劣势之处,这会让图像产生形变,或者图像变得过小,使一些特征产生了损失,继而对之后的特征选择产生巨大影响,所以引入了ROI Pooling. |
- 获得可能区域
- 对于这些区域进行resize,进行Rol Pooling,即输入的图像大小不固定,输出的feature map大小固定
- 输入到CNN
Faster R-CNN
Faster RCNN 与 Fast RCNN的区别主要是引入了区域生成网络RPN候选框提取模块。
1 | RPN的工作步骤如下: |
- 获得可能区域,使用RPN生成候选区域
- 对于这些区域进行resize,进行Rol Pooling
- 输入到CNN
L12
HDR
High Dynamic Range Imaging
Exposure:曝光\(Exposure=Gain\times Irradiance\times Time\)
- Gain:由ISO控制
- Irradiance:辐照度,由光圈aperture大小控制
- Time:由快门时间shutter speed控制
ISO:感光度
感光度是衡量底片对于光的灵敏程度,由敏感度测量学及测量数个数值来决定,国际标准化组织标准为ISO 6。对于光较不敏感的底片,需要曝光更长的时间以达到跟较敏感底片相同的成像,因此通常被称为慢速底片。高度敏感的底片因而称为快速底片。- Iso的副作用:由于噪声被放大,图像变得非常模糊。
拍照时,平均曝光应在传感器测量范围的中间。这样照片的明暗部分都有细节。
Dynamic Range
某一数值(如亮度)的最大值与最小值之比。
- 比如8位的RGB的图像的Dynamic Range就是256:1
- real world的Dynamic Range是100000:1
- 我们用了256:1的Dynamic Range来表示现实世界的100000:1的Dynamic Range
Image Formation Model
假设图像像素(x, y)的场景亮度为L(x, y)
- \(I(x,y)=clip[t_i*L(x,y)+noise]\)
曝光括弧:在不同曝光下捕捉多个LDR图像Lower Dynamic Range
合并:将它们合并成一个HDR图像
在每个图像中找到“有效的”像素:noise0.05<pixel<0.95clipping
适当地对有效像素值进行加权
权重如何确定?合理的像素值除以曝光时间\(pixel\ value/t_i\)
形成一个新的像素值作为有效像素值的加权平均值
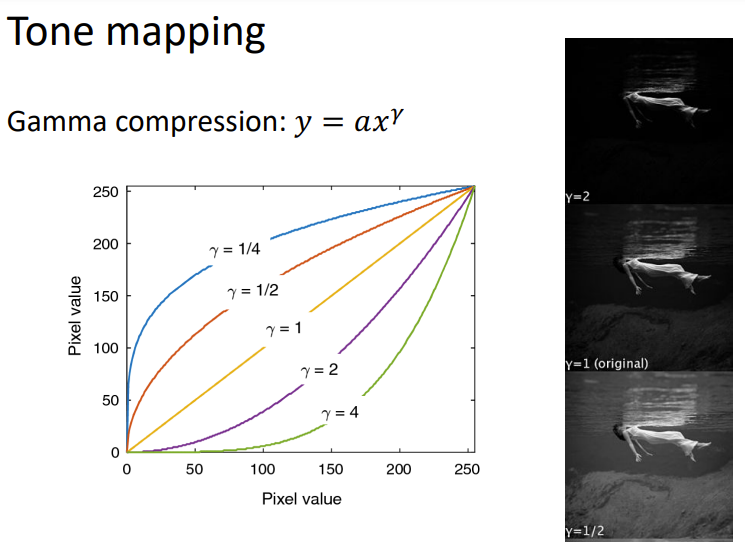
Tone Mapping如何将HDR图像12-bit在8-bit的SDR上显示?
- 线性压缩:\(X\rarr aX\)
- gamma压缩:\(X\rarr aX^\gamma\)
Deblurring
为什么会模糊
- 失焦:被摄对象不在景深内
- 运动模糊:移动的物体或不稳定的相机
如何获得更加清晰的图像
- 准确的焦点
- 快速的快门速度
- 大光圈导致模糊
- 高Iso导致模糊
- 使用硬件设备:三脚架、云台等
模糊的数学模型
散焦的模糊模式取决于光圈形状,抖动的模糊模式取决于相机的轨迹
- 模糊过程可以用卷积来描述
- blurred image = clear image × blur kernel
- 模糊后的图像称为卷积核
NBID
未知的clear image和已知的kernel
BID
未知的clear image和未知的kernel
对于NBID去卷积
\(G=F\otimes H\),F是我们要求的,G和H是已知的
我们对其进行傅里叶变换
\(FFT(G)=FFT(F\otimes H)=FFT(F)\times FFT(H)\)
\(FFT(F)=FFT(G)\div FFT(H)\)
逆傅里叶变换得到F
\(F=IFFT(FFT(G)\div FFT(H))\)
也可以用优化来计算
\(MSE=||G-F\otimes H||_2^2\)
Deconvolution is ill-posed
L12
GAN
GAN:生成对抗网络
- 生成网络:CNN等能够生成图片的网络
- 对抗网络:一个鉴别器,判别输入的图像是合成的图像还是真实的图像。
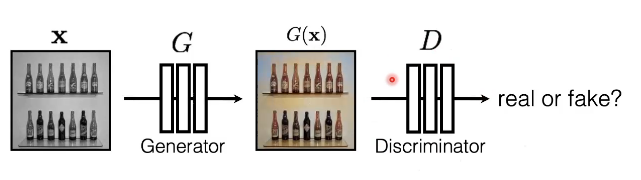
- D:Fake输出接近1,Real输出接近0
- GAN网络的训练:
- D的训练:\(argmax_D E_{x,y}[logD(G(x))+log(1-D(y))]\)
- G的训练:\(argmin_GE_{x,y}[logD(G(x))+log(1-D(y))]\)
- 一起训练:\(argmin_Gmax_DE_{x,y}[logD(G(x))+log(1-D(y))]\)
- D可以看作是训练G的损失函数
- 叫做对抗性损失
- 学习而不是手工设计
如果您喜欢此博客或发现它对您有用,则欢迎对此发表评论。 也欢迎您共享此博客,以便更多人可以参与。 如果博客中使用的图像侵犯了您的版权,请与作者联系以将其删除。 谢谢 !