机器学习
Lecture 1
赵洲,zhaozhou@zju.edu.cn,曹主415
1.1分数组成
- 大作业(图片分类):70%
- http://yann.lecun.com/exdb/mnist
- 思路PPT讲解:10
- 作业报告:30
- 编程代码:30
- DDL:15周周五晚上12点
- 小作业
- 阅读SVM开源算法报告:10
- DDL:8周周五晚上12点
- 阅读Transformer开源算法报告:10
- DDL:15周周五晚上12点
- 阅读SVM开源算法报告:10
- 课堂参与:10
- 签到20次,每次0.5%
1.2导论
- Machine Learning:经验驱动的性能提升的计算机系统
- Supervised监督学习:回归、分类
- Unsupervised非监督学习:聚类
- Reinforcement强化学习:游戏与控制
1.3监督学习
- Goal: 学习一个映射从输入x到输出y
- Training Data: labeled data有标签的输入输出对x,y
- 分类:离散的标签
- 回归:连续的标签
1.4非监督学习
- 只有输入,没有label
- Goal: find “interesting pattern”
- 隐因子:
- 降维
- 矩阵分解
- Topic Modeling
1.5强化学习
- 是延时的一个监督学习
- 这里的label是环境作用于机器的,是有延迟的reward
Lecture 2
2.1监督学习
【贝叶斯定理】\(P(A|B)=\frac{P(B|A)·P(A)}{P(B)}\)
- \(P(A|B)\)为后验概率,posterior
- \(P(B|A)\)为似然度,likelihood来自于model
- \(P(A)\)为先验Prior,来自label的比例
【Example】
| A | 0 | 0 | 1 | 1 | 1 | 0 |
|---|
先验
先验一般有两种情况:
- Uniform的情况\(P(w_1)=P(w_2)\)
- \(P(w_1)+P(w_2)=1\)
只根据先验的决策:
- 如果池塘里A鱼多,B鱼少,我们就猜测为A鱼
似然度
只根据likelihood的决策:
- likelihood从观测中的data中来
- 如果\(P(x|w_1)>P(x|w_2)\),预测为w1,x为一个特征
后验
贝叶斯公式\(P(w_i|x)=\frac{P(x|w_i)·P(w_i)}{P(x)}\)
概率公式\(P(x)=\sum_{i=1}^{k}P(x|w_i)P(w_i)\)
可以看到后验和先验×似然度成正比Posterior = likelihood×Prior
策略
选择后验概率最高,意味着错误率最小,即有最小错误率分类
- Decide \(w_i\),if \(P(w_i|x)>P(w_j|x)\)
- 在使用贝叶斯公式根据已知的先验和似然度来决策
- 可以加上ln便于计算
2.2参数估计
极大似然估计[一文搞懂极大似然估计 - 知乎 (zhihu.com)]
极大似然估计,通俗理解来说,就是利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值!
换句话说,极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。
对于分类器只能做参数估计,不能做模型估计,在参数估计中主要估计参数,模型是假定好的,比如假定是一个高斯模型,我们做的是估计高斯模型的一个参数,一个参数是\(μ\)一个是Σ,我们要估计的就是这两个参数。
似然函数\(p(x|\theta)\):
- 输入x为一个具体的数据,θ是模型的参数,
- 如果θ是已知的,x是变量那么这个函数是一个概率函数,它描述对于不同的样本点x,其出现概率是多少。
- 如果x是已知确定的, θ是变量,这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数,出现 x 这个样本点的概率是多少。
Example
假如有一个罐子,里面有黑白两种颜色的球,数目多少不知,两种颜色的比例也不知。我 们想知道罐中白球和黑球的比例,但我们不能把罐中的球全部拿出来数。现在我们可以每次任意从已经摇匀的罐中拿一个球出来,记录球的颜色,然后把拿出来的球 再放回罐中。这个过程可以重复,我们可以用记录的球的颜色来估计罐中黑白球的比例。假如在前面的一百次重复记录中,有七十次是白球,请问罐中白球所占的比例最有可能是多少?
很多人马上就有答案了:70%。而其后的理论支撑是什么呢?
我们假设罐中白球的比例是p,那么黑球的比例就是1-p。因为每抽一个球出来,在记录颜色之后,我们把抽出的球放回了罐中并摇匀,所以每次抽出来的球的颜 色服从同一独立分布。
这里我们把一次抽出来球的颜色称为一次抽样。题目中在一百次抽样中,七十次是白球的,三十次为黑球事件的概率是P(样本结果|Model)。
如果第一次抽象的结果记为x1,第二次抽样的结果记为x2....那么样本结果为(x1,x2.....,x100)。这样,我们可以得到如下表达式: \[ p(x_1,x_2,...,x_{100}|Model) \\=p(x_1|Model)p(x_2|Model)...p(x_{100}|Model) \\=p^{70}(1-p)^{30} \] 我们已经有了观察样本结果出现的概率表达式了。那么我们要求的模型的参数,也就是求的式中的p。那么我们怎么来求这个p呢?不同的p,直接导致P(样本结果|Model)的不同。
极大似然估计应该按照什么原则去选取这个分布呢?
- 采取的方法是让这个样本结果出现的可能性最大,也就是使得\(p^{70} (1-p)^{30}\)值最大,那么我们就可以看成是p的方程,求导即可!
- 求出p=70
MLE方法
- MLE即Maximum Likelihood Estimation
- 定义何为最优参数?观测到的sample出现的概率最大的参数
- 假设我们有c个training set,c个class
- 每一个class需要学习一个model,model参数为\(\theta_c\)
- MLE就是估计这个参数θ,要估计likelihood
- 就是说所有sample的概率乘起来最大,即似然函数
- \(P(D_c|\theta_c)=\prod_{x\in D_c}P(x|\theta_c)\)
- 其中Dc为c类样本组成的集合,参数θc对于数据集Dc的最大似然估计,就是寻找使得这个表达式最大的参数θ值。
- 假设我们模型是高斯模型,那么首先样本独立同分布
- \(p(x|w_i)=p(x|w_i,\theta_i)\)
- likelihood服从高斯分布\(p(x|w_i)\)~\(N(\mu_i,\Sigma_i)\)
- 似然函数\(P(D|\theta)=\prod_{k=1}^np(x_k|\theta)\)
- \(\theta=(\theta_1,...,\theta_c)\)
- 评估的θ需要最大化这个似然值
- 乘法难以评估,求导困难,取log
- 对于单个θ就是\(P(D_c|\theta_c)=\prod_{x\in D_c}P(x|\theta_c)\)
- \(l(\theta)=lnP(D|\theta)=\sum_{k=1}^nln\ p(x_k|\theta)\)
- 最后所求\(\theta^*={argmax}_{\theta}\ l(\theta)\)
- \(\nabla_{\theta}l(\theta)=[\frac{\partial}{\partial \theta_1},...,\frac{\partial}{\partial \theta_c}]^T=\sum_{k=1}^n\nabla_{\theta}ln\ p(x_k|\theta)\)
- 其中的\(p(x_k|\theta)\)是服从高斯分布的
- Σ固定,评估θ
- \(P(x)=-\frac{1}{\sqrt{2\pi \sigma}}e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2}\)
- \(\mu=x的均值\)
- \(\sigma^2=x的方差\)
- 高维的高斯
- \(P(x)=\frac{1}{(2\pi)^{\frac{d}{2}} |\Sigma|^\frac{1}{2}}exp[{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)}]\)
- d是维度
- \(\mu=\frac{1}{|D_c|}\sum_{x\in D_c}x\)
- \(\Sigma=\frac{1}{|D_c|}\sum_{x\in D_c}(x-\mu)(x-\mu)^T\)
- Σ固定,评估θ
- 令\(\nabla_{\theta}l(\theta)=0\)
- 【Example】固定Σ估计μ的高斯模型
- \(P(x|\mu)\)~\(N(\mu,\Sigma)\)
- \(ln\ p(x_k|\mu)=-\frac{1}{2}ln[(2\pi)^d|\Sigma|]-\frac{1}{2}(x_k-\mu)^T\Sigma^{-1}(x_k-\mu)\)
- 对参数μ求导
- \(\nabla_{\mu}ln\ p(x_k|\mu)=\Sigma^{-1}(x_k-\mu)\)
- 则\(\sum_{k=1}^n\Sigma^{-1}(x_k-\mu)=0\)
- 解出μ即可\(\mu^*=\frac{1}{n}\sum_{k=1}^nx_k\)
- 可以看到这个μ其实就是sample的均值
- 【Example】估计μ、Σ的高斯模型
- \(P(x|\theta)\)~\(N(\mu,\sigma^2)\)
- \(ln\ p(x_k|\theta)=-\frac{1}{2}ln(2\pi\sigma^2)-\frac{1}{2\sigma^2}(x_k-\mu)^2\)
- 对参数θ求导
- \(\nabla_{\theta}ln\ p(x_k|\theta)=\begin{bmatrix}\frac{\partial ln\ p(x_k|\theta)}{\partial\mu}\\\frac{\partial ln\ p(x_k|\theta)}{\partial\sigma^2}\end{bmatrix}=\begin{bmatrix}\frac{1}{\sigma^2}(x_k-\mu)\\ -\frac{1}{2\sigma^2}+\frac{(x_k-\mu)^2}{2\sigma^4}\end{bmatrix}=0\)
- \(\mu=\frac{1}{n}\sum x_k\)
- \(\sigma^2=\frac{1}{n}\sum(x_k-\mu)^2\)
- 令\(\overline{X}=[x_1-\mu,...,x_n-\mu]\)
- 则一般形式如下
- \(\mu=\frac{1}{n}\sum x_k\)
- \(\Sigma=\frac{1}{n}\overline{X}\overline{X}^T\)
- 【Example】
BE方法[贝叶斯估计 - 知乎 (zhihu.com)]
贝叶斯评估方法:
- 在MLE中,\(\theta_i\)是可以计算出一个固定的值的
- 极大似然估计是典型的频率学派观点,它的基本思想是:待估计参数 θ 是客观存在的,只是未知而已,当 \(θ^{mle}\) 满足“ \(θ=θ^{mle}\) 时,该组观测样本 (X1,X2,…,Xn)=(x1,x2,…,xn) 更容易被观测到“,我们就说 \(θ^{mle}\) 是 θ 的极大似然估计值。也即,估计值 \(θ^{mle}\) 使得事件发生的可能性最大。
- 在BE中,\(\theta_i\)是一个随机的变量
- 贝叶斯估计是典型的贝叶斯学派观点,它的基本思想是:待估计参数 θ 也是随机的,和一般随机变量没有本质区别,因此只能根据观测样本估计参数 θ 的分布。贝叶斯派的人认为,被估计的参数同样服从一种分布,即参数也为一个随机变量。他们在估计参数前会先带来先验知识,例如参数在 [0.5,0.6] 的区域内出现的概率最大,在引入了先验知识后在数据量小的情况下估计出来的结果往往会更合理。
- 我们需要计算后验概率分布\(P(\theta|D)\)
- 在MLE中,\(\theta_i\)是可以计算出一个固定的值的
为了计算后验概率分布,我们首先看到贝叶斯公式\(P(\theta|D)=\frac{P(D|\theta)P(\theta)}{P(D)}\)
- 那么有\(P(\theta|D)与P(D|\theta)P(\theta)\)成正比
- 其中\(P(\theta)\)为参数服从分布,即先验知识
- \(p(x|D)=\int p(x,\theta|D)d\theta=\int p(x|\theta,D)p(\theta|D)d\theta=\int p(x|\theta)p(\theta|D)d\theta\)
- 为什么要求\(p(x|D)\)?
【Example】未知μ的高斯分布generate出x的分布
- \(p(x|\mu)\)~\(N(\mu,\sigma^2)\)
- 假设\(p(u)\)~\(N(\mu_0,\sigma_0^2)\)
- 先求\(p(\mu|D)\)
- \(p(\mu|D)=\frac{p(D|\mu)p(\mu)}{\int p(D|\mu)p(\mu)d\mu}=\alpha\prod p(x_k|\mu)p(\mu)\\=\alpha'exp[-\frac{1}{2}(\sum(\frac{\mu-x_k}{\sigma})^2+(\frac{\mu-\mu_0}{\sigma_0})^2)]\\=\alpha''exp[-\frac{1}{2}[(\frac{n}{\sigma^2}+\frac{1}{\sigma_0^2})\mu^2-2(\frac{1}{\sigma^2}\sum x_k+\frac{\mu_0}{\sigma_0^2})\mu]]\)
- 这就求出了后验概率分布
- 并且之前假设的
- \(\mu_n=(\frac{n\sigma_0^2}{n\sigma_0^2+\sigma^2})\hat{x_n}+\frac{\sigma^2}{n\sigma_0^2+\sigma^2}\mu_0\)
- \(\sigma_n^2=\frac{\sigma_0^2\sigma^2}{n\sigma_0^2+\sigma^2}\)
- 再求\(p(x|D)\)后验密度即类条件概率密度
- 如上所述
- \(p(x|D)=\int p(x|\mu)p(\mu|D)d\mu\\=\frac{1}{2\pi \sigma \sigma_0}exp[-\frac{1}{2}\frac{(x-\mu_n)^2}{\sigma ^2+\sigma_0^2}]f(\sigma,\sigma_0)\)
- 其中\(f(\sigma,\sigma_0)=\int exp[-\frac{1}{2}\frac{\sigma^2+\sigma_0^2}{\sigma^2\sigma_0^2}(\mu-\frac{\sigma_n^2x+\sigma^2\mu_n}{\sigma^2+\sigma_n^2})^2]d\mu\)
- 得出结论为\(p(x|D)\)~\(N(\mu_n,\sigma^2+\sigma_0^2)\)
MAP方法
密度估计(Density Estimation)
怎么去给一个观测到的数据集估计出一个联合概率分布是比较常见的问题。比如说,给定一系列的观测值\(X=(x_1,x_2,...,x_n)\) , 每一个观测值都彼此独立的情况下,密度估计要选择一个概率分布模型,以及选择对应的最能够表达出X的联合概率的参数。最常见的两种方法有MAP和MLE(最大似然估计)。两种方法都要求找到并且优化一个模型以及它的参数来表达已知观测值。
在MAP中,在已知的概率分布模型和参数下,我们希望能够最大化观测到数据的可能性:\(P(X;\theta)=P(x_1,x_2,...,x_n;\theta)\) 所以我们要找到一组参数\(\theta\),让上面的式子的结果最大。
那么我们只需要\(max(P(X|\theta)P(\theta))\)
Discriminant Functions for the Normal Density判别函数
在分类器中,我们需要依据概率分类,而这个判断的一句就是根据判别函数获得的
- 一般形式
- 假设有c个类\(w_1,w_2,...,w_c\)
- 那么根据一个特征x,来查看\(p(w_i|x)\)的大小,取最大的为最后预测的类
- 即判别函数\(g(x)=p(w_i|x)\)
- 由贝叶斯公式知,\(p(w_i|x)\)~\(p(x|w_i)p(w_i)\)
- \(g(x)=p(x|w_i)p(w_i)\)
- 取对数
- \(g(x)=ln\ p(x|w_i)+ln\ p(w_i)\)
- 一般而言只要\(g(x)\)能够正确分类都可以作为判别函数
- g(x)不一定要计算出来,只要能够纵向比较大小即可
- 【Example】高斯分布下的一般形式的g(x)
- 判别函数\(g_i(x)=ln\ p(x|w_i)+ln\ p(w_i)\)
- \(p(x|w_i)=\frac{1}{(2\pi)^{\frac{d}{2}}|\Sigma_i|^\frac{1}{2}}exp[-\frac{1}{2}(x-\mu_i)^T\Sigma_i^{-1}(x-\mu_i)]\)
- \(g_i(x)=-\frac{1}{2}(x-\mu_i)^T\Sigma_i^{-1}(x-\mu_i)-\frac{d}{2}ln\
2\pi-\frac{1}{2}ln|\Sigma_i|+ln\ p(w_i)\)
- Case1:\(\Sigma_i=\sigma^2I\)
- \(g_i(x)=-\frac{(x-\mu_i)^T(x-\mu_i)}{2\sigma^2}+ln\ p(w_i)\)
- \(=-\frac{1}{2\sigma^2}(x^Tx-2\mu_i^Tx+\mu_i^T\mu_i)+ln\ p(w_i)\)
- 因为\(x^Tx\)对于所有的class都是相等的,等价于\(g(x)=w_i^Tx+w_{i0}\)
- \(w_i=\frac{\mu_i}{\sigma^2}\)
- \(w_{i0}=-\frac{\mu_i^T\mu_i}{2\sigma^2}+ln\ p(w_i)\)
- 这是一个线性的函数
- 最后来查看两个类的输出相等的情况
- \(g_i(x)=g_j(x)\)
- \(0=(\frac{\mu_i-\mu_j}{\sigma^2})^Tx-\frac{\mu_i^T\mu_i-\mu_j^T\mu_j}{2\sigma^2}+ln\frac{p(w_i)}{p(w_j)}\)
- 假设\(p(w_i)=p(w_j)\)
- \(x_0=\frac{1}{2}(\mu_i+\mu_j)\)
- Case2:\(\Sigma_i=\Sigma\)
- \(g(x)=-\frac{1}{2}(x^T\Sigma^{-1}x-2\mu_i^T\Sigma^{-1}x+\mu_i^T\Sigma^{-1}\mu_i)+ln\ p(w_i)\)
- 因为\(x^T\Sigma^{-1}x\)对所有的类都是一样的,等价于\(g_i(x)=\mu_i^T\Sigma^{-1}x-\frac{1}{2}\mu_i^T\Sigma^{-1}\mu_i+ln\
p(w_i)\)
- \(g_i(x)=w_i^Tx+w_{i0}\)
- 分界线
- \(g_i(x)=g_j(x)\)
- \(0=(\mu_i-\mu_j)^T\Sigma^{-1}x-\frac{\mu_i^T\Sigma^{-1}\mu_i-\mu_j^T\Sigma^{-1}\mu_j}{2}+ln\ \frac{p(w_i)}{p(w_j)}\)
- 参数估计
- \(\mu_i=\frac{1}{N_i}\sum_{j\in w_i}x_j\)
- \(P(w_i)=\frac{N_i}{N}\)
- \(\Sigma=\sum_{i=1}^c\sum_{j\in w_i}\frac{(x_j-\mu_i)(x_j-u_i)^T}{N_i}\)
- Case3:\(\Sigma_i=Arbitrary\)
- \(g_i(x)=-\frac{1}{2}(x^T\Sigma_i^{-1}x-2\mu_i^T\Sigma_i^{-1}x+\mu_i^T\Sigma_i^{-1}\mu_i)-\frac{1}{2}ln\ |\Sigma_i|+ln\ P(w_i)\)
- \(g_i(x)=x^TW_ix+w_i^Tx+w_{i0}\)
- Case1:\(\Sigma_i=\sigma^2I\)
2.3 Naive Bayes Classifier朴素贝叶斯
给出\(x=(x_1,x_2,...,x_p)^T\)
给出一系列特征,我们希望找到这些特征最可能出现的类
即\(P(w|x)=P(w|x_1,...,x_p)\)
- 又\(P(w|x)\)~\(P(x_1,...,x_p|w)P(w)\)
- 特征独立
- \(P(x_1,...,x_p|w)=P(x_1|w)...P(x_p|w)\)
- 那么我们只需要找到最大的概率进行预测即可
【Example】
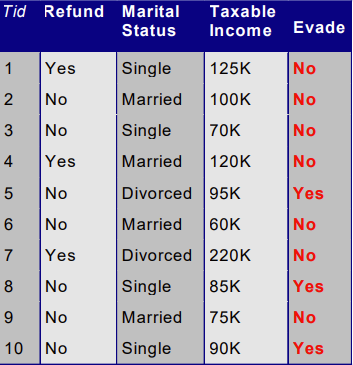
现在我们给出一个记录X=(Refund=No,Married,Income=120K),使用朴素贝叶斯预测其类别
首先,类别只有两个:Yes,No
\(P(w_k)=\frac{N_k}{N}\)每个类别的先验概率
- \(P(NO)=\frac{7}{10}\)
- \(P(YES)=\frac{3}{10}\)
\(P(x_i|w_k)=\frac{|x_i|}{N_k}\)每个类别中特征出现的概率
\[ P(Refund=YES|NO)=\frac{3}{7}\\ P(Refund=NO|NO)=\frac{4}{7}\\ P(Refund=YES|YES)=0\\ P(Refund=NO|YES)=1 \]
$$ P(Married|YES)=0\ P(Divorced|YES)=\ P(Single|YES)=\
P(Married|NO)=\ P(Divorced|YES)=\ P(Single|YES)=\ $$
工资是高斯分布的,我们首先估计参数
- \(P(x|w_i)\)~\(N(\mu,\sigma^2)\)
- \(\mu=\frac{1}{n_x}\sum x_i=110\)
- \(\sigma^2=\frac{1}{n_x}\sum(x_i-\mu)^2=2975\)
\(P(X|NO)=P(x_1|NO)P(x_2|NO)P(x_3|NO)=0.0024\)
\(P(X|YES)=0\)
\(P(X|NO)P(NO)>P(X|YES)P(YES)\)
Class=NO
Laplace smoothing
- \(P(x_i|w_k)=\frac{|x_{ik}|+1}{N_{w_k}+K}\)
Lecture 3
3.1 Linear Method for Regression
Linear Model
- 目标是学习一个从输入x到输出y的一个映射
- y是离散的,分类
- y是实数值,回归
- 【Example】
- 设\(x\in R^d,x=[x_1,...,x_d]^T\)
- 参数\(w=[w_1,...,w_d]^T\in R^d,b\)
- 那么我们可以写出方程\(f(x)=w^Tx+b\)
- 进一步令\(x=[x_1,..,x_d,1]^T\)
- \(w=[w_1,...,w_d,b]^T\)
- \(f(x)=w^Tx\)
Polynomial Curve Fitting
- 用多项式拟合数据参数为\(a=(a_0,a_1,...,a_m)\)
- \(f(x,a)=a_0+a_1x_1+...+a_mx^m\)
- Zero Order Polynomial
- 是一个constant
- 其实就是均值
- First Order Polynomial
- 用一条直线拟合
- Third Order Polynomial
- 用三次函数的拟合
- 次数越高越复杂,精度高,容易过拟合
MSE Criterion均方误差判据
- 考察一个函数拟合是否好,我们用误差函数来判断
- 需要拟合的训练数据为\((x_1,y_1),...,(x_n,y_n)\)
- 学习到的函数为\(f(x,a)\)
- \(MSE(a)=\frac{1}{n}\sum_{i=1}^n(y_i-f(x_i,a))^2\)
- 最小化MSE,即最小化标签\(y_i\)和输出预期\(f(x_i)\)方差,这里的f被参数a决定
- \(J_n(a)=\sum_{i=1}^n(y_i-a^Tx_i)^2\)
- 最小化\(a^Tx_i\)和\(y_i\)的均方误差
- 使用矩阵表示
- \(X=[x_1,x_2,...,x_n]\)
- \(y=[y_1,y_2,...,y_n]^T\)
- \(J_n(a)=(y-X^Ta)^T(y-X^Ta)\)
3.2Linear Regression Model
- 训练数据为\((x_i,y_i)\),标签为\(y_i\)
- 学得的模型为\(f(x)=a_0+\sum_{i=1}^pa_ix_i=a_0+a^Tx\)
- \(a=[a_1,...,a_p]^T,x\)为特征向量
- 接下来我们要最小化误差
- MSE均方误差
- \(J_n=\frac{1}{n}\sum_{i=1}^n(y_i-f(x_i))^2\)
- RSS残差平方和
- \(RSS(f)=\sum_{i=1}^n(y_i-f(x_i))^2\)
- MSE均方误差
- 以MSE均方误差为例,如何最小化?
- 使用矩阵表示
- \(X=[x_1,x_2,...,x_n]\)
- \(y=[y_1,y_2,...,y_n]^T\)
- \(J_n(a)=(y-X^Ta)^T(y-X^Ta)\)
- 对a求导
- \(\frac{dAX}{dX}=A^T\)
- \(\frac{dx^Tx}{dx}=2x\)
- \(\nabla J_n=-2X(y-X^Ta)\)
- \(a=(XX^T)^{-1}Xy\)
- 使用矩阵表示
- 则我们就求出了使得MSE最小化的a
- \(\hat y=X^Ta=X^T(XX^T)^{-1}Xy\)
3.3 Statistical Model of Regression
- 生成的模型:\(y=f(x,a)+\epsilon\)
- \(f(x,a)\)是一个确定性函数
- \(\epsilon\)是一个随机的噪声,它可以有一个概率分布,比如\(\epsilon\)~\(N(0,\sigma^2)\)
- 【Example】
- \(y=f(x,a)+\epsilon\)
- \(\epsilon\)~\(N(0,\sigma^2)\)
- 给定\(a,X,\sigma\)的条件下,输出y的概率
- 即\(y-f(x,a)\)的概率,因为\(f(x,a)\)是给定的
- \(p(y|x,a,\sigma)=\frac{1}{\sigma \sqrt{2\pi}}exp[-\frac{1}{2\sigma^2}(y-f(x,a))^2]\)
- 接下来使用最大似然估计MLE求a
- \(L(D,a,\sigma)=\prod_{i=1}^n p(y_i|x_1,a,\sigma)\)
- \(a^*=argmax\prod_{i=1}^np(y_i|x_i,a,\sigma)\)
- 使用对数似然函数
- \(l(D,a,\sigma)=log(L(D,a,\sigma))=log\prod p(y_i|x_i,a,\sigma)=\sum_{i=1}^nlog\ p(y_i|x_i,a,\sigma)\)
- \(l(D,a,\sigma)=-\frac{1}{2\sigma^2}\sum_{i=1}^n(y_i-f(x_i,a))^2+c(\sigma)\)
- 到最后还是最小化\(RSS(f)\)
Overfitting
- model不能过于简单也不能过于复杂,即参数的复杂度
- 过简单,欠拟合,在训练集上就表现不好
- 过复杂,过拟合,在训练集上良好,在测试集上表现差
- 我们可以对参数的限制放入损失函数中,作为正则函数项
Ridge Regression
- 使用损失函数+正则项
- \(a^*=argmin_{a}\sum_{i=1}^n(y_i-x_i^Ta)^2+\lambda\sum_{j=1}^p a_j^2\)
- 需要挑选合适的\(\lambda\)
- 等价形式
- \(a^*=argmin_{a}\sum(y_i-x_i^Ta)^2\)
- Subject to \(\sum_{i=1}^n a_j^2≤t\)
- L2正则化
- \(C=C_0+\frac{\lambda}{2n}\sum_ww^2\)
- L1正则化
- \(C=C_0+\frac{\lambda}{n}\sum|w|\)
- L1比L2更加sparse
- 求解以\(a^*=argmin_{a}\sum_{i=1}^n(y_i-x_i^Ta)^2+\lambda\sum_{j=1}^p
a_j^2\)为例
- 矩阵表示\((y-X^Ta)^T(y-X^Ta)+\lambda a^Ta\)
- 求导\(-2X(y-X^Ta)+2\lambda a\)
- 求解\(a^*=(XX^T+\lambda I)^{-1}Xy\)
Bayesian Linear Regression
- \(P(a|D)=\frac{P(D|a)P(a)}{P(D)}\)
- 假设a是高斯分布
- \(p(a)=N(a|0,\lambda^{-1}I)\)
- \(ln(p(a))=-\frac{\lambda}{2}a^Ta+c\)
- 那么计算Posterior时我们可以先计算出likelihood
- \(l(D,a,\sigma)=-\frac{1}{2\sigma^2}\sum_{i=1}^n(y_i-f(x_i,a))^2+c(\sigma)\)
- \(ln(p(a))=-\frac{\lambda}{2}a^Ta+c\)
- 那么后验是正比于likelihood×prior的,在log下就是相加
- 相当于多了一个正则项
3.3 LASSO
- Least Absolute Selection and Shrinkage Operator
- \(\hat \beta=argmin\frac{1}{2n}\sum
(y_i-x_i^T\beta)^2\)
- subject to \(\sum_{j=1}^p|\beta_j|≤t\)【L1】
- subject to \(\sum_{j=1}^p\beta_j^2≤t\)【L2】
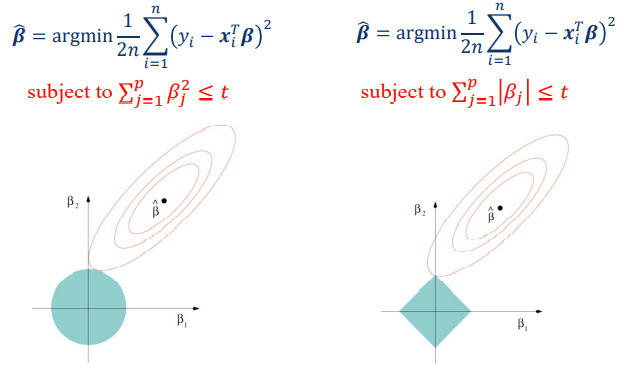
LASSO Solution
- \(\hat \beta=argmin\frac{1}{2n}\sum (y_i-z_i\beta)^2\)
- 这里的z是x经过归一化的,y也是归一化的
- \(\sum y_i=0\)
- \(\sum z_i=0\)
- \(\frac{1}{n}\sum_iz_{ij}^2=1\)
- \(f(\beta)=\frac{1}{2n}(y-\beta z)^T(y-\beta z)+\lambda|\beta|\)
- \(f(\beta)=\frac{1}{2n}z^Tz\beta^2-\frac{1}{n}<z,y>\beta+\frac{1}{2n}y^Ty+\lambda |\beta|\)
- \(2<z,y>=y^Tz+z^Ty\)
- 且\(\hat \beta=argmin\frac{1}{2n}\sum (y_i-x_i^T\beta)^2\)
- 去除与\(\beta\)无关项,\(f(\beta)=\frac{1}{2}\beta^2-\frac{1}{n}<z,y>\beta+\lambda |\beta|\)
- \[ f(\beta)= \begin{cases} \frac{1}{2}\beta^2-(\frac{1}{n}<z,y>-\lambda)\beta,\quad \beta\geq 0\\ \frac{1}{2}\beta^2-(\frac{1}{n}<z,y>+\lambda)\beta, \quad \beta\lt 0 \end{cases} \tag{1} \]
- \(\beta^*=\begin{cases}\frac{1}{n}<z,y>-\lambda,\quad \frac{1}{n}<z,y>\gt \lambda\\ 0,\quad|\frac{1}{n}<z,y>|\leq\lambda\\\frac{1}{n}<z,y>+\lambda,\quad \frac{1}{n}<z,y><-\lambda\end{cases}\)
3.4 Model Assessment and Selection
- 模型的评估和模型的选择:
- 泛化性、准确度
- 在新的data上测试集上进行测试
3.5 Bias-variance Decomposition
- 偏差-方差分解(Bias-Variance Decomposition)是统计学派看待模型复杂度的观点。Bias-variance分解是机器学习中一种重要的分析技术。给定学习目标和训练集规模,它可以把一种学习算法的期望误差分解为三个非负项的和,即样本真实噪音noise、bias和 variance。
- noise 样本真实噪音是任何学习算法在该学习目标上的期望误差的下界;( 任何方法都克服不了的误差)
- bias 度量了某种学习算法的平均估计结果所能逼近学习目标的程度;(独立于训练样本的误差,刻画了匹配的准确性和质量:一个高的偏差意味着一个坏的匹配)
- variance 则度量了在面对同样规模的不同训练集时,学习算法的估计结果发生变动的程度。(相关于观测样本的误差,刻画了一个学习算法的精确性和特定性:一个高的方差意味着一个不稳定的匹配)。
【Example】
- 给出标签数据\((x_i,y_i)\)
- 学到一个函数\(f(x)=y\)
- Loss:\(L(y,f(x))\)
- 期望误差:
- \(E(L)=\int\int L(y,f(x))p(x,y)dxdy\)
- 若将平方误差用于Loss
- \(L(y,f(x))=(y-f(x))^2\)
- 获得EPE(Expected Prediction Error)
- \(EPE(f)=\int \int (y-f(x))^2p(x,y)dxdy\)
- 那么我们获得了平方误差下的期望误差即EPE
- 又\((y-f(x))^2=(y-E(y|x)+E(y|x)-f(x))^2\)
- \(=(y-E(y|x))^2+(E(y|x)-f(x))^2+2(y-E(y|x))(E(y|x)-f(x))\)**<*>**
- 则\(\int\int
(y-E(y|x))^2p(x,y)dxdy=\int_x\int_y(y-E(y|x))^2p(y|x)\ dy\
p(x)dx=\int_xvar(y|x)p(x)dx\)
- 运用公式01
条件期望与条件方差 - 简书 (jianshu.com):
- \(E(y|x)=\int y\ p(y|x)dy\)
- \(var(y|x)=\int (y-E(y|x))p(y|x)dy\)
- 运用公式01
条件期望与条件方差 - 简书 (jianshu.com):
- 则\(\int \int
(E(y|x)-f(x))^2p(x,y)dxdy=\int_yp(y|x)dy\int_x(E(y|x)-f(x))^2p(x)dx=\int(E(y|x)-f(x))^2p(x)dx\)
- 运用公式
- \(\int p(y|x)dy=1\)
- \(E(y|x)\)与y无关
- 运用公式
- 则\(\int \int
(y-E(y|x))(E(y|x)-f(x))p(x,y)dxdy=0\)
- \(\int \int yE(y|x)p(x,y)dxdy=\int_x\int_yy\ p(y|x)dy\ E(y|x)p(x)dx=\int_xE(y|x)^2p(x)dx\)
- \(\int \int yf(x)p(x,y)dxdy\)
- \(\int \int E(y|x)^2p(x,y)dxdy=\int_yp(y|x)dy\int_xE(y|x)^2p(x)dx=\int_xE(y|x)^2p(x)dx\)
- \(\int\int E(y|x)f(x)p(x,y)dxdy=\int_yp(y|x)dy\int _xE(y|x)f(x)p(x)dx=\int_x\int_yy\ p(y|x)dyf(x)p(x)dx=\int \int yf(x)p(x,y)dxdy\)
- \(EPE(f)=\int(E(y|x)-f(x))^2p(x)dx+\int var(y|x)p(x)dx\)
- 在实际中,往往会给数据集D
- \(f(x)=f(x;D)\)
- \(EPE(f)=\int(f(x;D)-E(y|x))^2p(x)dx+\int var(y|x)p(x)dx\)
- 其中的\((f(x;D)-E(y|x))^2\)可以如上一样分解
- \((f(x;D)-E(y|x))^2=E_D\{[f(x;D)-E_D(f(x;D))]^2\}+\{E_D(f(x;D))-E(y|x)\}^2\)
- \(bias^2=\int\{E_D(f(x;D))-E(y|x)\}^2p(x)dx\)
- \(variance=\int E_D\{[f(x;D)-E_D(f(x;D))]^2\}p(x)dx\)
- \(noise=\int var(y|x)p(x)dx\)
Lecture 4
4.1 Discriminant Functions and Classifiers
- 对于判别函数\(g_i(x)\),分类器会把特征x归入\(w_i\)类,如果满足\(g_i(x)>g_j(x)\),对所有的\(i\neq j\)成立
Sigmoid Function(Logistic Function)
- \(\sigma(t)=\frac{1}{1+e^{-t}}\)
- 输入的值可以在正无穷和负无穷之间,但是输出在0,1之间,可以看作一个概率
- 即\(\sigma:R\rarr(0,1)\)
4.2 Logistic Regression
- 逻辑回归LR是一种用sigmoid函数估计概率来描述一类因变量与一个或几个自变量之间关系的分类模型。
- 假设二分类问题
- \(y_i\)是第i个label,a是参数
- \(P(y_i=1|x_i,a)=\sigma(a^Tx_i)=\frac{1}{1+e^{-a^Tx_i}}\)
- \(P(y_i=-1|x_i,a)=1-\sigma(a^Tx_i)=\frac{1}{1+e^{a^Tx_i}}\)
- \(P(y_i|x_i,a)=\sigma(y_ia^Tx_i)=\frac{1}{1+e^{-y_ia^Tx_i}}\)
- 使用最大似然估计去估计a
- \(P(D)=\prod_{i\in I}\sigma(y_ia^Tx_i)\)
- \(l(P(D))=\sum_{i=I}log(\sigma(y_ia^Tx_i))=-\sum_{i\in I}log(1+e^-{y_ia^Tx_i})\)
- 则\(E(a)=\sum_{i\in I}log(1+e^{-y_ia^Tx_i})\)
- 最小化误差函数
- Logistic Regression
- \(E(a)=\sum_{i\in I}log(1+e^{-y_ia^Tx_i})\)
- \(E(a)\)是上凸还是下凸?
- Linear Regression
- \(E(a)=\sum_{i\in I}(y_i-a^Tx_i)^2\)
- Logistic Regression
- 使用梯度下降法
4.3 Gradient Descent
- 一般采用一阶的优化方法,即使用一阶导数
- 一般只能找到局部最优解
一般的步骤
- 目标函数\(J(w)\),可以是多变量也可以是多变量的,可微的
- 下降最快的方向是a处梯度的反方向,即\(-\nabla J(a)\)
- 更新a,\(b=a-\gamma \nabla J(a)\),γ为学习率或者步长,要足够小
- 我们一开始猜一个权重参数\(w_0\)
- \(w_{n+1}=w_n-\gamma \nabla J(w_n)\)
- 更新参数
- 那么\(J(w_i)\)就会不断下降
1 | begin initialize a,theta,eta,k=0 |
线性近似
- \(E(a+\Delta a)=E(a)+E'(a)\Delta a+E''(a)\frac{\Delta a^2}{2!}+...\)
- Gradient Decent
- \(\Delta a=-\eta E'(a)\)
- Newton Method
- 二阶的方法
- 让\(E'(a)\Delta a+E''(a)\frac{\Delta a^2}{2!}\)最小
- \(\Delta a=-\frac{E'(a)}{E''(a)}\)
4.4 支持向量机
- 线性可分的数据,我们需要分开
- 正类:\(w^Tx+b\leq0\)
- 负类:\(w^Tx+b\geq 0\)
- 正好在边界:\(w^Tx+b=0\)
- 怎么分类比较好?如何定义这个好?
- 边际使得离两种类别的点都比较远
几何边缘
- 假设\(\gamma\)是x到边界线的距离
- 设\(x_0\)是x在边界线上的投影
- \(x=x_0+y\gamma \frac{w}{||w||}\)
- \(x_0\)在分界线上
- \(\gamma = y\frac{w^Tx+b}{||w||}\),这里的y是区分正负类的
- 那么支持向量的\(y(w^Tx+b)=1\)
- 其他数据点的\(y(w^Tx+b)\geq1\)
- 我们最大化两个支持向量的距离\(D=\frac{y(w^Tx+b)}{||w||}\)
- 则最大化\(\frac{2}{||w||}\)
- 即最小化\(\frac{1}{2}||w||\)
- 去掉根号
- 得到优化问题\(min\frac{1}{2}||w||^2,y_i(w^Tx_i+b)≥1\)
松弛变量
- 允许数据值离开支持向量一段距离
- \(min_{w,b}\frac{1}{2}||w||^2+C\sum_{i=1}^n\xi_i\)
- \(y(w^Tx_i+b)\geq1-\xi_i\)
- \(\xi_i\geq0\)
求解
- \(\xi_i\geq1-y(w^Tw_i+b)\)则\(\xi_i=max[1-y(w^Tx_i+b),0]\),即是损失函数
- \(min\{\sum_{i=1}^nmax[1-y(w^Tx_i+b),0]+\frac{1}{2C}||w||^2\}\)
- \(l (f)=max[1-f,0]\),Hinge Loss
- SVM就是一个HingeLoss作为损失函数,正则为L2Norm的优化
- Linear Regression:Square Loss \(l(f)=(y-f)^2=(1-yf)^2\)
- Logistic Regression:Logistic Loss \(l(f)=log(1+e^{-yf})\)
General Formulation of Classifiers分类范式
- \(min_f\{\sum_{i=1}^nl(f)+\lambda R(f)\}\)
- Loss Function
- Square、Logistic、Hinge
- Regularizer
- L1、L2
Lecture 5
5.1 Deep Learning 概述
- 深度学习是机器学习的一个分支
- 基于representations学习,表征学习,使用多层神经网络的非线性转换来学习
- 与Supervised Learning区别
- Collect training samples
- Define feature(更重要)
- Design and Train Model
- Predict
5.2 Neural Network
Linear Model(Classifier)
Perceptron
- 是Linear的,加上一个激活函数
- Sample:\(x\in R^d,x=[x_1,...,x_d]^T\)
- DrawBack,只能学习线性可分的函数
Backpropagation Algorithm反向传播算法
Activation Function激活函数
- Sigmoid
- \(\sigma(s)=\frac{1}{1+e^{-s}}\)
- \(\frac{d\sigma(s)}{ds}=\sigma(s)(1-\sigma(s))\)
- Tanh
- ReLU
- \(ReLU(z)=\begin{cases}z,\quad z\geq0\\0,\quad otherwise\end{cases}\)
- \(ReLU(z)=max(0,z)\)
- 缓解梯度消失问题
- Leaky ReLU
- ELU
- PReLU
5.3 Convolution卷积
图像的输入
- 对于200*200的图像,用全连接输入,第一层需要200*200个units,则输入参数有200*200*200*200个
- 卷积神经网络
- 权重共享
- 一个unit不再覆盖全部的图像,而是部分图像local feature
何为卷积
- 输入:一个图像
- 卷积核:一个可学习的参数w
- Feature Map:即输出的特征图
- 卷积操作:
- \(s[i,j]=(x*w)[i,j]\)
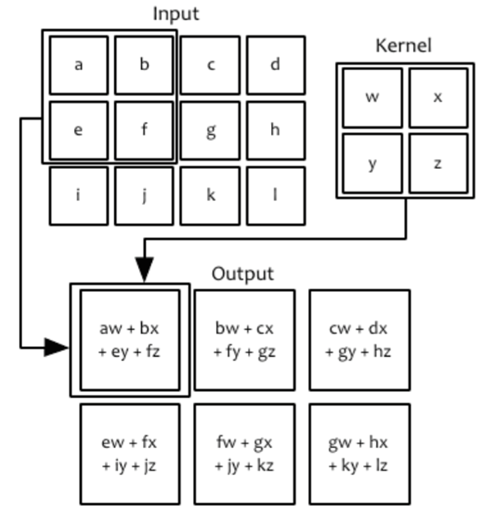
卷积层
- 输入图像:height*width*depth
- 32*32*3
- filter滤波器:height*width*depth
- 5*5*3,卷积生成28*28*1的特征图
- 可以有多个滤波器进行卷积
- 用6个5*5*3的filter进行卷积,生成28*28*6的特征图
- 卷积后需要进行输入激活函数
池化层
- Pooling用于降维
- MaxPooling:取最大的
- AveragePooling:取平均
Lecture 6
6.1 Clustering
- 无监督学习
- 我们只有输入没有label,即只有x,没有y,不能使用MLE来评估
- 目标是找到interesting patterns
- 引入伪标签概念,不是真的label,只是把一群data聚在一起给他们一个label
- 先打伪标签,再训练再打伪标签
- EM:专门为无监督学习的
Clustering
- 做的事情是把空间中的data分为两处,分为两个pattern
- 聚类不一定要知道聚类个数K
- Cluster
- 在Group中相似
- 在Group外不相似
6.2 K-Means
- 假设有K个聚类,随机选择K个data points作为种子点\(\mu_k\)
- 递归进行以下过程,直到收敛
- Assign each point to the cluster with the nearest seed
point,给每一个data打上伪标签,根据是目前的model中的\(\mu_k\)
- \(z_i=argmin_k||x_i-\mu_k||^2\)
- Update the seed point for each cluster,第k类的中心更新
- \(\mu_k=\frac{1}{N_k}\sum_{i=1}^{N_k}x_i^{(k)}\)
- Assign each point to the cluster with the nearest seed
point,给每一个data打上伪标签,根据是目前的model中的\(\mu_k\)
- 复杂度分析
- N个point,d为维度,K为聚类数,t是迭代数
- 时间复杂度\(O(tNKd)\)
- Centroid是聚类的中心,可以上是空间上的任意一点。
- Medoid是聚类的中心,但是是point上的一个
K-Medoids
给出K和D,D为pairwise distance matrix。
- 随机选取K个数据点作为种子点
- 递归进行以下步骤
- Assign每一个点,离种子点最近的。伪标签
- 更新种子点,种子点要保持为data中的一点。update
- How to find the medoid
- 计算中心点\(\mu\)
- 找到离\(\mu\)最近的点
- 复杂度:\(O(tN(k+1)d)\)
6.3 Gaussian Mixture Model
- 假设model是有K个高斯分布,我们要估计参数
- \(\mu_k,\Sigma_k,\pi_k\)分别是高斯分布的两个参数,和第k个模型产生这个data的先验概率
- 在之前的MLE中,我们已经知道了data是由哪个分布生成的,在这里我们并不知道
- \(p(x;\Theta)=\sum_{k=1}^K\pi_kp_k(x;\theta_k)\)这里就是Mixture,每个数据点都是由一个模型生成的,但是我们不知道具体是哪个,因此需要一个概率参数进行估计
- \(\Theta=\{\pi_1,...,\pi_k,\theta_1,...,\theta_k\},\sum_{k=1}^K\pi_k=1\)
- \(p_k(x;\theta_k)=N(x;\mu_k,\Sigma_k)\)
- 用log-likelihood解会非常难解
- \(log\prod p(x^{(i)};\Theta)=\sum_{i=1}^Nlog(\sum_{k=1}^K\pi_kN(x^{(i)};\mu_k,\Sigma_k))\)
- 我们可以用琴生不等式解出下界
参数估计
- 引入伪标签变量\(z_k\)
- \(P(z_k)=\pi_k\)
- \(P(x_i,z_i)=P(x_i|z_i)P(z_i)\)
- \(P(x_i|z_i=k)\)是高斯的\(N(\mu_k,\Sigma_k)\)
- 初始的\(\pi_k,\mu_k,\Sigma_k\)是随机的
E Step 打伪标签
- 算后验,\(Q_k^{(i)}=P(z^{(i)}=k|x^{(i)})\)
- \(=\frac{p(x^{(i)}|z^{(i)}=k)P(z^{(i)}=k)}{p(x^{(i)})}\)
- 其中\(p(x^{(i)}|z^{(i)}=k)\)是服从高斯分布的
- 其中\(P(z^{(i)}=k)=\pi_k\)
- 其中\(p(x^{(i)})=\sum_k p(x^{(i)}|z^{(i)}=k)p(z^{(i)}=k)\)
M Step 更新参数
- 多了\(Q_k\),MLE是没有\(Q_k\)直接更新的
- \(\mu_k=\frac{\sum_i Q_k^{(i)}x^{(i)}}{\sum_i Q_k^{(i)}}\)
- \(\Sigma_k=\frac{\sum_i Q_k^{(i)}(x^{(i)}-\mu_k)(x^{(i)}-\mu_k)^T}{\sum_i Q_k^{(i)}}\)
- \(\pi_k=\frac{\sum_iQ_k^{(i)}}{n}\)
6.4 EM
- Convex Set:一个集合是Convex的,仅当集合两点中的任一点都在集合中
- \(any \ x_1,x_2\in C,\ \theta x_1+(1-\theta)x_2\in C,\ \theta\in(0,1)\)
- Convex Function:凸函数,下凸
- \(f(\theta x_1+(1-\theta)x_2)\leq\theta f(x_1)+(1-\theta)f(x_2)\)
- Concave Function:凹函数,上凸
- 与凸函数相反
Jensen不等式
- 若f为凸函数,则满足
- \(f(\sum_{i=1}^n\lambda_ix_i)\leq\sum_{i=1}^n\lambda_if(x_i)\)
- 其中\(\lambda_i\geq0,\sum\lambda_i=1\)
- 即\(f(E[x])\leq E[f(x)]\)
- 那么我们就可以解之前的最大似然函数
- \(log\prod p(x^{(i)};\Theta)=\sum_{i=1}^Nlog(\sum_{k=1}^K\pi_kN(x^{(i)};\mu_k,\Sigma_k))\)
- 可以不断计算它的low bound,因为log是凹的!
6.5 Problem Description
- 我们的模型是\(P(x,z,\theta)\)但是我们只观测到x
- log似然函数
- \(l(\theta)=\sum_{i=1}^nlog\sum_zP(x_i,z;\theta)\)
- 设\(Q(z_k)\)是后验概率即\(Q(z_k)=P(z_k|x_i,\theta)\)
- \(\sum_z Q(z)=1\)
- \(L(\theta)=\sum_{i=1}^n log \sum_z P(x_i,z;\theta)=\sum_{i=1}^nlog\sum_zQ(z)\frac{P(x_i,z;\theta)}{Q(z)}\)
- \(\geq\sum_{i=1}^n\sum_zQ(z)log\frac{P(x_i,z;\theta)}{Q(z)}=l(\theta)\)
- 其中\(P(x_i,z,\theta)/Q(z)\)是一个constant
- \(P(x_i,z,\theta)/Q(z)=P(x_i,\theta)\)
6.6 EM算法总结
- E :\(Q(z)=P(z|x^{(i)};\theta)\)
- M:\(\theta=argmax_{\theta}\sum_{i=1}^m\sum_zQ(z)log\frac{p(x^{(i)},z^{(i)};\theta)}{Q(z)}\)
6.7 Density-Based Clustering Method
Lecture 7
降维技巧
- 什么是降维?
- 从x到z的特征映射
- x是原始representation,通常是高维的
- z的维度更低,从而进行降维
Linear and Nonlinear
Linear Transformation
- \(\mathcal{F}(x\in R^n)=z\in R^d\)
- z是d维的,每一个维度的值都是有一个projection函数决定的
- \(f_1(x)=z_1,...,f_d(x)=z_d\)
- f是线性的,\(a_i^Tx=z_i\)
- \(A=[a_1,...,a_d],A^Tx=z\)
- \(A^T\in R^{d\times p}:x\in R^p\rarr z=A^Tx\in R^d\)
- A怎么学习?无监督学习,有监督学习
Feature Extraction VS Feature Selection
- Selection:选择最好的subset
PCA主成分分析
这是一种无监督学习的降维,核心思想点是降维的表示的信息不要丢弃,保持信息,因为没有信息,因此我们需要保留信息。
variance要尽量大,从而进行特征信息的保存。用于Compression和classification。
Retain most of the sample's information:定义什么是sample's information?是variation。
将二维降到一维的任务
对n个data做降维,我们假设有p维的n个数据\(\{x_1,...,x_n\}\)
假设线性transformation:\(z_i^{(1)}=a_1^Tx_i\),这里的1?
我们要优化a,让var(z)最大
\(var(z^{(1)})=E((z^{(1)}-\overline{z}^{(1)})^2)\)
\(=\frac{1}{n}\sum(a^T_1x_i-a^T_1\overline x)^2\)
\(=\frac{1}{n}\sum a^T_{1}(x_i-\overline x)(x_i-\overline x)^Ta_1=a_1^TSa_1\)
\(S=\frac{1}{n}\sum(x_i-\overline x)(x_i-\overline x)^T\)
我们要做的就是\(max_{a_1}a_1^TSa_1\)
假设\(a_1^Ta_1=1\)
\(L=a_1^TSa_1+\lambda(a_1^Ta_1-1)\)
求导\(Sa_1=\lambda a_1\)
那么\(a_1\)就是特征向量
LDA Linear Discriminant Analysis
监督降维,并且需要分类,有标签的类,在降维后还是要分类
类内距离小,类间距离大,就是目标函数,假设有两个类
\(z=a^Tx\)
\(\overline \mu_i=\frac{1}{n}\sum_{z\in w_i}z\)
\(\mu_i=\frac{1}{n}\sum_{x\in w_i}x\)
\(\overline \mu_i=a^T\mu_i\)
我们的目标函数\(\frac{(\overline \mu_1-\overline\mu_2)^2}{S_1^2+S_2^2}\)
\(s_i^2=\sum_{y\in w_i}(y-\overline \mu_i)^2=\sum_{x\in w_i}(a^Tx-a^T\mu_i)^2=\sum_{x\in w_i}(a^Tx-a^T\mu_i)(a^Tx-a^T\mu_i)^T\)
\(=\sum_{x\in w_i}a^T(x-\mu_i)(x-\mu_i)^Ta=a^TS_ia\)
within-class sactter matrix:\(S_w=S_1+S_2,s_1^2+s_2^2=a^TS_wa\)
between-class sactter matrix:\(S_B=a^TS_Ba\)
那么最大化\(J(a)=\frac{a^TS_Ba}{a^TS_wa}\)
LPP Locality Preserving Projection
局部保持,只定义两个data point是不是邻居
\(x\in R^p \rarr a^Tx=z\)
\(W\in R^{n*n},w_{ij}=\begin{cases}1,x_i和x_j是邻居\\0\end{cases}\)
\(min\sum_{ij}w_{ij}(z_i-z_j)^2=min\sum_{ij}w_{ij}(a^Tx_i-a^Tx_j)^2\)
我们只需要最小化原始空间中为邻居的点的距离
\(=min\sum_{ij}w_{ij}a^T(x_i-x_j)(x_i-x_j)^Ta=min\ a^T\sum_{ij}w_{ij}(x_ix_i^T-x_ix_j^T-x_jx_i^T+x_jx_j^T)a\)
\(=min\ a^TXLX^Ta\)
\(L=D-W\)
\(\sum_{ij}w_{ij}()()^T=XWX^T\)
Lecture 8
非监督学习
传统的技术,隐因子发掘的技术
- 主题建模
- 矩阵分解
主题建模
- 是一个统计模型,发现隐主题
- 应用:
- 文本生成
- 信息检索
词袋模型
- 我们简化了词的顺序信息,没有顺序信息
- 只考虑这个词是否出现在文档中
- 可以考虑频率等统计信息
定义
- 词:\(w\),词的集合
- 文本:\(d=\{w_1,...,w_n\}\),一系列词构成的集合
- 一系列文本:\(D=\{d_1,...,d_N\}\),一系列文本
- 每个词的产生是独立的
- \(p(w)=\theta_w=\frac{n_w}{\sum_v^V
n_v}\)词的频率就是概率,相当于先验,\(n_v\)是第v个词出现在文本中的频数
- \(\sum_v^V \theta_w=1\)
- \(p(D;\theta)=\prod_{i=1}^Np(d;\theta)=\prod_{i=1}^N\prod_{j=1}^np(w_j)=\prod_{w}^V\theta_w^{n_w}\)
- 最大似然
- \(l(\theta)=\sum_{w}^V n_wlog\theta_w\)
- \(p(w)=\theta_w=\frac{n_w}{\sum_v^V
n_v}\)词的频率就是概率,相当于先验,\(n_v\)是第v个词出现在文本中的频数
Document-Term Matrix
传统的文档词汇的建模
D是所有文档的集合,\(d_i\)是文档,\(w_j\)是每一个词,W为词的集合
矩阵维度\(|D\times W|\)
在矩阵的(i,j)上存了一个频率,即第j个词在第i个文档的出现的频率,一般来说这个矩阵会比较稀疏
对文档进行降维,我们想让他从词汇的空间到一个主题的空间
- Polysemy:一词多义
- vector space model不能区分一词多义
- Synonymy:同义词
- 同义词在vector space model中没有联系
- topic和words,topic是低维的,words是高维的
Language Model Paradigm in IR
模型做什么?后验概率
定义
- \(R_d\in\{0,1\}\) d是否相关
- \(q\subseteq \Sigma\):查询一系列的查询关键词
- \(P(R_d=1|q)=\frac{P(q|R_d=1)P(R_d=1)}{P(q)}\)
- \(P(R_d=1|q)\)
- 给定一个查询q,第d个文档相关的概率
- 对于词是离散的不是连续的不能用高斯模型
- \(P(q|R_d=1)\)为了搜索相关文档d而生成搜索关键词q的概率
- 之前的似然度是从高斯模型中计算的,是连续的
- 查询的似然度,从文本中进行采样,确定了文章的主题,一些词汇的频率会比较高
- 实际中如何获得?
- \(P(q|R_d=1)=P(q|d)\)
- \(q=\{w_1,...,w_q\}\)
- \(P(q|d)=\prod P(w_i|d)\)
- \(\hat P(w_i|d)=\frac{n(d,w)}{\sum_{w'}n(d,w')}\)
- \(P(R_d=1)\)文档中的先验
- 实际中使用流行度,即文章被搜索到的概率,对一个网站来说,如果说许多重要的网站链接到了用这个网站,那么这个网站是流行的
- 与查询无关,与流行度有关
PLSA
Probabilistic Latent Semantic Analysis 无监督降维,用隐因子表示
Documents\(\rarr\)Latent Concepts\(\rarr\)Terms
\(\hat P(w|d)=\sum_zP(w|z)P(z|d)\)
文档是很难产生词的。我们引入隐变量z,我们先预估文档是关于什么主题的,对于每个主题,产生词的概率是怎么样的。
- 给出一个文档,它的主题概率分布如何?\(P(z|d;\theta)\)
- 给出一个主题,它的词的概率分布如何?\(P(w|z;\pi)\)
\(l(\theta,\pi;N)=\sum_{d,w}n(d,w)log(\sum_zP(w|z;\theta)P(z|d;\pi))\)
Lecture 9
SVD奇异值分解
- 求法
PCA:奇异值分解SVD,复杂度很大,没有并行算法。
对于任意一个矩阵\(X\in R^{m\times n}\),存在一个分解
\(X=U\Sigma V^T\)
\(U\in R^{m\times m},V\in R^{n\times n},U^TU=UU^T=1,V^TV=VV^T=1\)
\(\Sigma\in R^{m\times n}\)为对角阵
\(U\)为\(AA^T\)的特征向量构成的,\(V\)是\(A^TA\)特征向量构成的
\(\Sigma^2=\Sigma^T\Sigma=\Lambda\)
其中\(A^TA=V\Lambda V^T,AA^T=U\Lambda U^T\)
\(\sigma_i\)是\(XX^T\)的按照递减次序排列的非零特征值的算术平方根
SVD可以计算最优近似解,即低秩的近似运算
\(X^*=argmin_{rank(\overline X)=k}||X-\overline X||_F^2\)
SVD的解:
\(X^*=Udiag\{\sigma_1,..,,\sigma_k,0,...,0\}V\)
- 近似的原理是,奇异值会越来越小,我们将小的值作为0、
- 这里的k我们可以自己选择
当k=d时,\(\Sigma = diag\{\sigma_1,...,\sigma_d\}\)
\(\sigma_1\geq \sigma_2\geq...\geq \sigma_d\gt 0\)
矩阵分解
\(X\in R^{m\times n}\),\(X=UV\)
\(\begin{bmatrix}x_{11}\ x_{21}\ ...\ x_{n1}\\x_{12}\ x_{22}\ ...\ x_{n2}\\...\\x_{1m}\ x_{2m}\ ...\ x_{nm}\end{bmatrix}_{m*n}=\begin{bmatrix}u_{11}\ u_{21}\ ...\ u_{k1}\\u_{12}\ u_{22}\ ...\ u_{k2}\\...\\u_{1m}\ u_{2m}\ ...\ u_{km}\end{bmatrix}_{m*k}\times \begin{bmatrix}v_{11}\ v_{21}\ ...\ v_{n1}\\v_{12}\ v_{22}\ ...\ v_{n2}\\...\\v_{1k}\ v_{2k}\ ...\ v_{nk}\end{bmatrix}_{k,n}\)
\(U\in R^{m\times k}\)
\(V\in R^{k\times n}\)
分解后,X中的每一列,即列向量\(x_i\)都能表示为U中列向量\(u_1,...,u_k\)的线性组合
- \(x_i=v_{i1}u_1+...+v_{ik}u_k\)
- \(X=[x_1,...,x_n]=UV=U[v_1,...,v_n]\)
- \(x_i\in R^m,v_i\in R^k\)
- \(x_i=Uv_i\)
每一个V中的列向量,可以看作X的低维的表示,将m维降维k维
如果存在一个矩阵\(A\in R^{k\times m}\),满足
- \(AU=I\)
- 那么\(Ax_i=v_i\)
【主题建模】
在主题建模中也可以使用矩阵分解
\(P(w|d)=\frac{n(d,w)}{\sum_{w'}n(d,w')}\),在文档d中词w的出现概率等于文档中w的个数除以文档中词的总个数。条件概率,对d文档,我们多大概率采样w这个词
\(\sum_i P(w_i|d)=1\)
放入矩阵
\(X=\begin{bmatrix}P(w_1|d_1)\ ... P(w_1|d_n)\\...\\P(w_m|d_1)\ ...\ P(w_m|d_n)\end{bmatrix}\)
进行分解,原先文档的特征是文档的词的分布,即我们用一个向量表示了文档,第\(i\)个文档的各个词的出现的概率在\(x_i\)中被体现。用词表示太过于稀疏,我们使用矩阵分解,用主题表示。
\(\hat P(w|d)=\sum_z P(w|z)P(z|d)\)
\(\hat X=\begin{bmatrix}\hat P(w_1|d_1)\ ... \hat P(w_1|d_n)\\...\\\hat P(w_m|d_1)\ ...\ \hat P(w_m|d_n)\end{bmatrix}\)
\(U=\begin{bmatrix}\hat P(w_1|z_1)\ ... \hat P(w_1|z_k)\\...\\\hat P(w_m|z_1)\ ...\ \hat P(w_m|z_k)\end{bmatrix}\)
\(V=\begin{bmatrix}\hat P(z_1|d_1)\ ... \hat P(w_1|z_k)\\...\\\hat P(w_m|z_1)\ ...\ \hat P(w_m|z_k)\end{bmatrix}\)
用k维的主题进行表示:
- 对于一个文档,主题分布如何\(P(z|d)\)的矩阵
- 对于一个主题来说,词的分布如何\(P(w|z)\)的矩阵
\(X≈\hat X=UV\)
NMF非负矩阵分解
- Assumption
- Low rank
- Nonnegative
- \(X\in R^{m\times n}\),\(\hat X=UV^T≈X\)
Cost Function
- 欧几里得距离
- \(||A-B||^2=\sum_{i,j}(a_{ij}-b_{ij})^2\)
- Divergence
- \(D(A||B)=\sum_{ij}(A _{ij}log\frac{A_{ij}}{B_{ij}}-A_{ij}+B_{ij})\)
- 一般是逼近概率值,而不是数据点
NMF Optimization
\(min||X-UV^T||^2,s.t. u_{ij}\geq 0,v_{ij}\geq 0\)
\(J=||X-UV^T||^2=tr((X-UV^T)^T(X-UV^T))\)
\(J=tr(X^T-X^TUV^T-VU^TX+VU^TUV^T)\)
\(L=tr(X^TX)-2tr(X^TUV^T)+tr(VU^TUV^T)+tr(\Gamma U^T)+tr(\Phi V^T)\)
\(\frac{\partial L}{\partial U}=-2XV+2UV^TV+\Gamma\)
\((UV^TV)_{ik}u_{ik}-(XV)_{ik}u_{ik}=0\)
\(u_{ik}\leftarrow \frac{(XV)_{ik}}{(UV^TV)_{ik}}u_{ik}\)
同理
\(v_{jk}\leftarrow \frac{(X^TU)_{jk}}{(VU^TU)_{jk}}u_{jk}\)
Lecture 10
Transformer
性能比CNN、RNN等都要好,而且能够统一空间特征和时间特征到同一个网络。既可以做时间序列的特征抽取也可以做空间数据的特征抽取。
Transformer的架构图:
- 目前大部分人们的神经序列转换模型都有Encoder-Decoder结构。Encoder将输入序列映射到一个连续表示序列。编码和解码的网络。
- 对于编码得到的,Decoder每次解码生成一个符号,直到生成完整的输出序列
- RNN有一个问题:我们会有遗忘问题,对于编码的越长的数据,我们会遗忘之前的信息,解码时只能使用近几个信息,前面的信息被遗忘了
- 对于一词多义现象:
- 聚焦模型:解码一个信息不仅仅要根据编码对应位置的信息,还要周围的信息,即判断环境。
- 对于每一步解码,模型信息都是自回归的,即在生成下一个符号时将先前生成的符号作为附加输入。
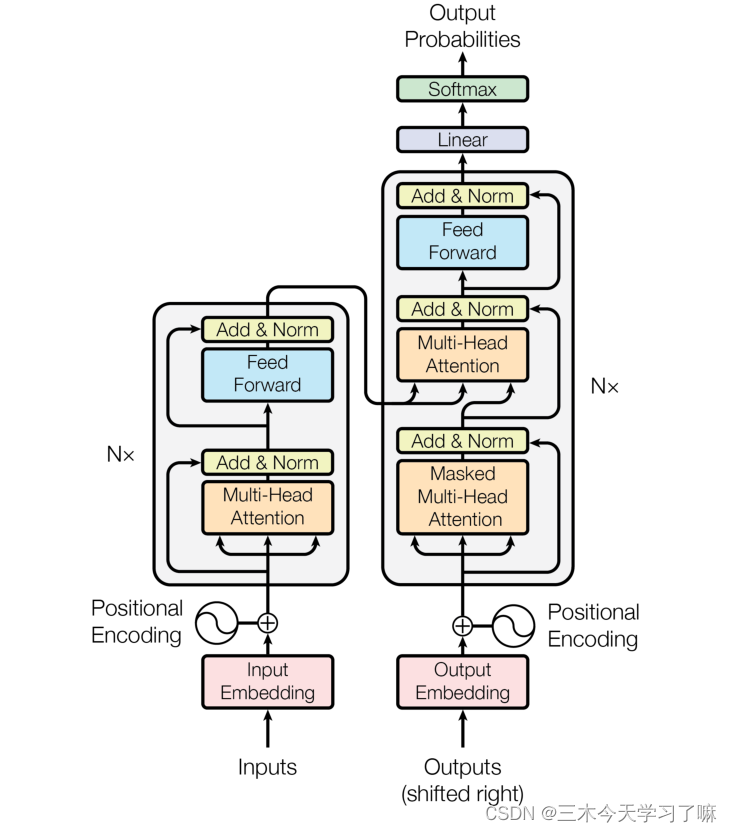
模型结构
详解Transformer (Attention Is All You Need) - 知乎 (zhihu.com)
输入和输出
之前的RNN和CNN都是编码解码架构,Transformer也是这么一个架构,有编码器和解码器
词袋模型的机制是:词的顺序不影响对句子的理解,但是实际中是影响的
传统机器学习都是词袋模型,但是这不符合我们的预期,因此我们需要有序列
例如翻译问题,输入“Why do we work?”进入编码器
得到隐藏层输出到解码器,输入开始信号,输出“为”
再输入“为”,再输出“什”,即要依赖于原序列的数据、同时依赖于已解码的数据,就是说我们这里是自回归的。因为前后的解码结果有一定的关联性,因此我们依赖解码的词来进行下一步解码有助于提高准确度。
Attention机制
这是transformer的灵魂,有很多种Attention机制
你需要知道Attention - 知乎 (zhihu.com)
Self-Attention和Transformer - 知乎 (zhihu.com)
QKV模型
最简单的是QKV模型,Qurey,Key,Value。
假设输入是q,在memory中我们以(key,value)的形式存储上下文
- 例如K是一个question,V是一个answer,Q是一个新的question,那么我们就会检索memory中的哪个K更与Q相似,再输出相似的K的V就是答案。给出一个新的问题,并不是检索Value和Q的相似度,而是K和Q的相似度。
- 在Memory中找相似
score function:\(e_i=a(q,k_i)\)- 对每一个K,计算相似度
- 归一化:\(\alpha_i=softmax(e_i)\),映射到概率
- 相似度大的,概率大
- 读取内容:\(c=\sum_{i}\alpha_i
v_i\)
- 输出对Value加权求和
- 在Memory中找相似
Attention机制是用来干嘛的
- 借鉴了生物在观察和学习行为过程中,建立起对事物的需要重点观察或学习的区域,来获取全局信息
- 我们没有办法同时处理所有事情,会有优先级,注意力就会有一个权重值,从而更专注的聚焦到某些关键信息上。
Self-Attention自聚焦机制
之前的RNN等序列编码,只解决了前面一项的数据的影响,未考虑后向的编码的影响,解决方法双向的RNN、LSTM等,即解决了前项依赖和后项依赖,但是遗忘问题仍未解决。
Self-Attention本质上是一种特殊的Attention,要解决传统算法的问题。依赖较远的问题,在一句话中可以很好地学习场景表达。只考虑一个序列内部的聚焦机制。
权重w并不是一个需要神经网络学习的参与,假设有两个element,不一定挨在一起,有距离,来源于\(x_i,x_j\)的计算结果
\(w_{ij}'=x_i^Tx_j\)关联度,即重要程度
\(w_{ij}=\frac{exp(w_{ij}')}{\sum_jexp(w_{ij}')}\)根据关联度生成权重
AT和SA的不同之处
- AT经常被应用于从编码器到解码器
- SA比较擅长在一个序列中,寻找不同部分的关系
- AT可以连接两种不同的模态,如图片和文字;SA更多应用在统一模态上
- SA可以在一个模型中被多次独立使用。
QKV聚焦机制
Attention函数可以将Query和一组Key-Value对映射到输出,其中QKV和输出都是向量。输出是值的加权和,其中分配给每个Value的权重由Query与相应的Key兼容函数计算。
这种机制称为Scaled Dot
\(Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt d_k})V\)
获得一个加权的特征向量。
\(d_k\)为维度
Trick1 :对于SA可以加入学习参数\(W_q,W_k,W_v\)
\(q_i=W_qx_i\)
\(k_i=W_kx_i\)
\(v_i=W_v x_i\)
\(x_i是raw\_data\),即输入的数据
\(w_{ij}'=q_ik_j^T\)计算score
归一化,除以\(\sqrt d_k\)
对score使用softmax激活函数
softmax点乘value值v,得到加权的每个输入向量的评分\(v\)
相加之后得到\(z=\sum v\)
Trick 2:为什么有根号?
- Softmax函数对非常大的输入很敏感,梯度传播出现问题,导致学习速度下降,导致学习停止
- 用\(\sqrt d_k\)来对输入的向量进行缩放,放置softmax的函数增长过大
Trick 3:Multi-Head Attention
- 相当于h个不同的self-attention的集成
- 将输入的X输入到h个self-attention中,得到h个加权后的特征矩阵
- 特征矩阵经过全连接得到输出Z
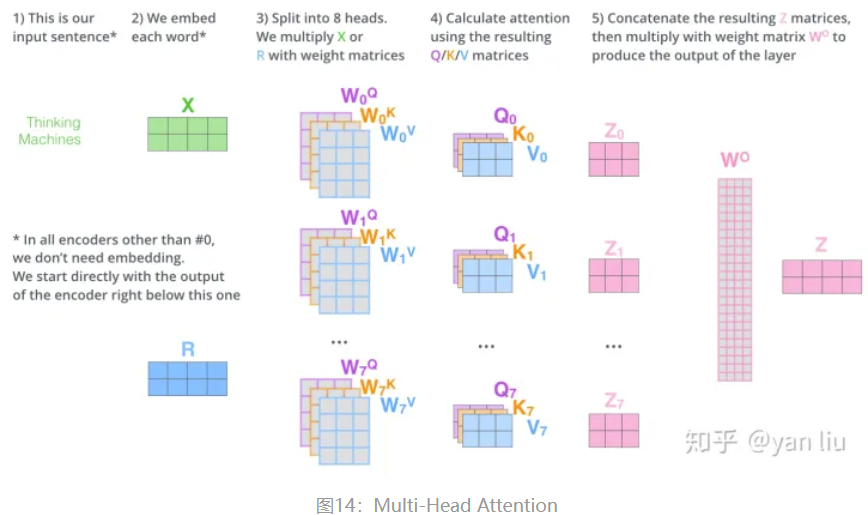
- \(Multihead(Q,K,V)=Concat(head_1,...,head_h)W\)
- \(head_i=Attention(QW_i^Q,KW_i^K,VW_i^V)\)
Lecture 11
Tokenize
第一步就是tokenize函数
定义一个正则,输入一个句子,输出一些列词语。
[Input Embedding][https://www.jianshu.com/p/e6b5b463cf7b]
输入编码,输入是
- 词的大小vocab_size
- 模型维度d_model:对于词,计算机难以看懂,用向量和数值表达词语
定义一个矩阵,矩阵大小是vocab_size行,一行d_model个值,词语转化为向量的一个矩阵。
如何考虑到词的顺序?
Position Encoder
使用PE来表示词的顺序,即对词语的位置进行编码。
输入编码矩阵:embedding vector*input words的矩阵,词的嵌入矩阵,词的表示的局长那你
位置编码矩阵:不同的位置用不同的向量表示embedding vector*max_seq_len的矩阵
带有位置信息的输入编码 = 输入编码+位置编码矩阵对应位置的向量
- 如何赋予其位置
- i是编码维度,pos为位置
- 对
pos in range(max_seq_len)每一个位置- \(PE_{(pos,2i)}=sin(pos/10000^{2i/d_{model}})\)
- \(PE_{(pos,2i+1)}=cos(pos/10000^{2i+1/d_{model}})\)
Transformer Block
self-attention layer
- 对于attention函数
- 首先获得\(score=\frac{QK^T}{\sqrt d_k}\)
- softmax函数激活
- 返回softmax(score)*V
- 多头聚焦机制
- 定义三个投射矩阵
- 使用多头机制
- 对于attention函数
normalization layer
如何做layer norm
使得梯度更加平稳
```pseudocode input X in R^{Bd} output y in R^{Bd} mu_B = 1/B sum(X) sigma_B^2 = 1/B sum((X-mu_B)^2) X' = (X-mu_B)/sigma_B Y = gamma·X'+beta //gamma beta是要学习的
1
2
3
4
5
6
7
8
9
10
11
- feed forward layer
- 选择4倍大小作为我们feedforward层的维度,这个值使用的越小就越节省内存,但是相应的表示性也会变差。
```python
self.ff = nn.Sequential(
nn.Linear(k,4*k),
nn.ReLU(),
nn.Linear(4*k,k)
)Transformer Block的forward
1
2
3
4
5def forawrd(self,x):
attended = self.attention(x)
x = self.norm1(attended+x)//残差
fedforward = self.ff(x)
return self.norm1(fedforward+x)//残差
another normalization layer
Lecture 12
解码时使用编码的结果,不能使用自聚焦机制。
解码器的输入是上一轮的输出,因此解码器不能并行,只能串行。
Encoder
输入:
- vocab_size词的个数
- d_model模型的维度
- N编码有多少的Transformer Block
- heads多头注意力机制的多少个头
- dropout防止过拟合
- 获得编码矩阵
- 初始化位置编码
- 堆砌N个Encoder Layer,即N个Block
- Encoder Layer
- normalization
- attention
- dropout&normalization
- feed forward
- normalization
- Encoder Layer
- 最后进行Normalization
Decoder
结构和Encoder差不多,多了一个attention和sub-layer
输出:对应i位置的输出词的概率分布
输入:encoder输出和对应的i-1位置的decoder输出。中间的attention不是self-attention,它的K,V来自于Encoder,Q来自于
- normalization
- mask attention,mask未解码的部分,解码部分使用自注意力机制学习
- dropout&normalization
- attention:利用编码信息
- dropout&normalization
Masked Multi-Head Attention
只希望前侧的上下文对注意有影响,不希望后侧的上下文对注意的影响。因为说话时,我们不能通过没有说的话对现在说的进行推理。
只使用已经输出的词对其进行理解聚焦。如何让后面的词对现在的此没有影响?我们让相似度足够小,即权重小,那么对应的元素对我们的影响小。
自注意力机制SA
- 在Encoder中使用
- 对于一个元素来说,我们可以从其前后的上下文来理解,帮助解码K=V=Q
掩码注意力机制MSA
- 在Decoder中使用
- 对于一个元素来说,我们只从其前的上下文来理解,帮助解码K=V=Q
Attention
- 将Decoder进行Attention到Encoder的结果
CNN in Transformer
输入图片\(H*W*C\),对图片分块,每个块长度\(P*P\),有\(N=H*W/(P*P)\)块
每一块展成一维向量,长度为\(P*P*C\)
总输入变换\(N*(P^2*C)\)
Patch Embedding
线性变化,全连接层,压缩维度从patch_dim到dim
Position Embedding
位置编码没有用传统的cos和sin编码,而是采用随机初始化,之后训练出来。
Cls Token
分类任务,对于图片分类或者句子分类,需要学习的是全局表征。
ViT只用了Encoder编码器结构,缺少解码过程,因此给了额外的一个用于分类的向量,与输入进行拼接。
Lecture 13
Dropout
为什么会有Dropout?
overfitting一种现象
- 训练集和测试集分布不同;
- 训练集并没有真多"训练",而是记忆到了网络中
不希望所有的神经元一起学习,希望删掉一些神经元后还是可以进行学习。解决两个神经元耦合的问题,避免两个神经元协同学习,某种程度上对神经网络进行解耦。
dropout网络,在参数传入前进行一个randam mask,从而进行dropout。
\(r_j^{(l)}\)~\(Bernoulli(p)\)
\(\hat y^{(l)}=r^{(l)}*y^{(l)}\)
\(z_i^{(l+1)}=w_i^{(l+1)}\hat y^{(l)}+b_i^{(l+1)}\)
\(y^{(l+1)}=f(z_i^{(l+1)})\)
本质上是机器学习的方法。数据太少,用dropout会欠拟合,数据太多,dropout没有作用。
模型平局:Dropout是模型平均的一种
- 对于每次输入的样本,其对应的网络结构都是不同的,取平均会让过拟合和欠拟合结果相互抵消。
- Dropout策略使得网络共享权重,因此训练测试时间代价低。
减少单元共适应:Dropout策略使得每个单元不一定每次训练都在同一个网络中,从而可以解耦原先单元们之间的依赖关系,提高网络的鲁棒性。
Lecture 14
Batch Normalization and Layer Normalization
批归一化Batch Normalization BN
解决神经网络内部协变量偏移的问题,加速网络收敛速度。
Internal Covariate Shift

每次用一个mini-batch来优化网络,每一个p都会学到一个分布,容易学到带方差的。

- 通过规范化手段,把每层神经网络输入值的分布(每个特征)强行拉回均值为0,方差为1的标准正态分布
- 使得激活函数的输入值落到敏感区域内,使得梯度变大,避免梯度消失问题。
- 一般Batch Normalization操作是在激活函数之前的。
如何实现批归一化?


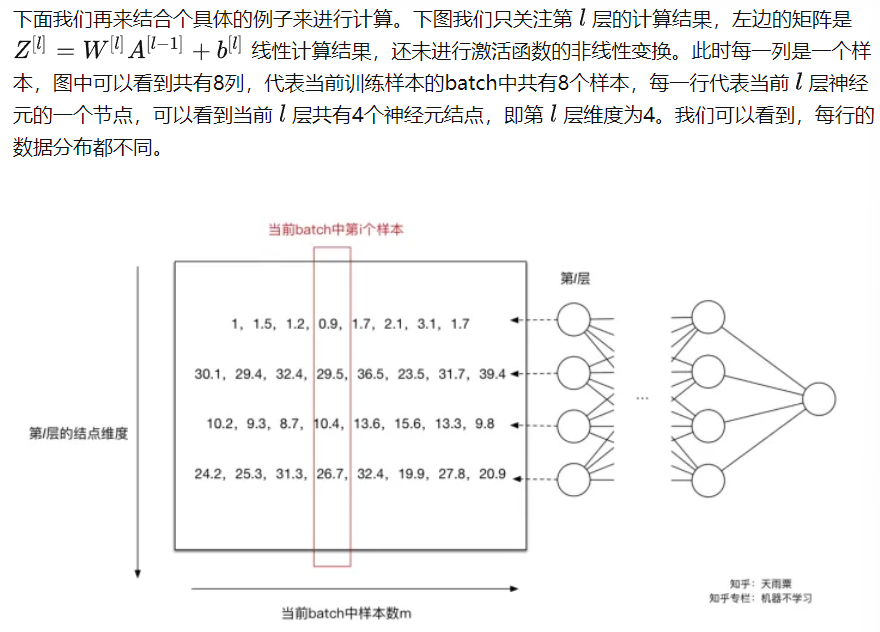

批处理可学习。
如同上面提到的,Normalization操作我们虽然缓解了ICS问题,让每一层网络的输入数据分布都变得稳定,但却导致了数据表达能力的缺失。也就是我们通过变换操作改变了原有数据的信息表达(representation ability of the network),使得底层网络学习到的参数信息丢失。另一方面,通过让每一层的输入分布均值为0,方差为1,会使得输入在经过sigmoid或tanh激活函数时,容易陷入非线性激活函数的线性区域。
因此,BN又引入了两个可学习(learnable)的参数 γ 与 β ,这两个参数的引入是为了恢复数据本身的表达能力,对规范化后的数据进行线性变换,即 \(Z_j=γ_jZ_j+β_j\) 。特别地,当 \(γ^2=σ^2\),β=μ 时,可以实现等价变换(identity transform)并且保留了原始输入特征的分布信息。
加上拉伸和偏移的参数,可以学习。归一化导致数据表达能力的遗失,因此我们使用两个参数进行学习。使用反向传播和梯度下降求\(\beta,\gamma\)。

类比为一摞书,这摞书总共有 N 本,每本有 C 页,每页有 H 行,每行 W 个字符。BN 求均值时,相当于把这些书按页码一一对应地加起来(例如第1本书第36页,第2本书第36页…),再除以每个页码下的字符总数:N×H×W,因此可以把 BN 看成求“平均书”的操作(注意这个“平均书”每页只有一个字),求标准差时也是同理。
层归一化LN
如果batchsize比较小,均值和方差估计有偏,效果较差。
把一个 batch 的 feature 类比为一摞书。LN 求均值时,相当于把每一本书的所有字加起来,再除以这本书的字符总数:C×H×W,即求整本书的“平均字”,求标准差时也是同理。
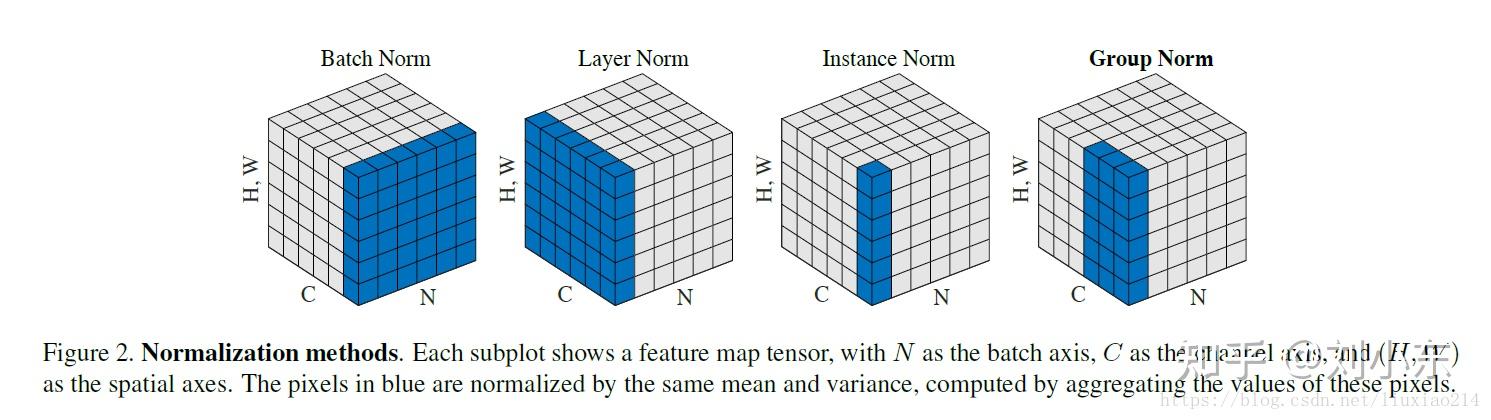
与BN不同的是,LN对每一层的所有神经元进行归一化,与BN不同的是:
LN中同层神经元输入拥有相同的均值和方差,不同的输入样本有不同的均值和方差;
BN中则针对不同神经元输入计算均值和方差,同一个batch中的输入拥有相同的均值和方差。
LN不依赖于batch的大小和输入sequence的深度,因此可以用于batchsize为1和RNN中对边长的输入sequence的normalize操作。
一般情况,LN常常用于RNN网络!
总结
Batch Normalization 批规范化
Feature-Map:\(x\in R^{N*C*H*W}\),有N个样本,样本是C通道的,高为H,宽为W
对其求均值和方差时,将在 N、H、W上操作,而保留通道 C 的维度。具体来说,就是把第1个样本的第1个通道,加上第2个样本第1个通道 ...... 加上第 N 个样本第1个通道,求平均,得到通道 1 的均值(注意是除以 N×H×W 而不是单纯除以 N,最后得到的是一个代表这个 batch 第1个通道平均值的数字,而不是一个 H×W 的矩阵)。求通道 1 的方差也是同理。对所有通道都施加一遍这个操作,就得到了所有通道的均值和方差。
- \(\mu_c(x)=\frac{1}{NHW}\sum_{n=1}^{N}\sum_{h=1}^{H}\sum_{w=1}^Wx_{nchw}\)
- \(\sigma_c(x)=\sqrt{\frac{1}{NHW}\sum_n\sum_h\sum_{w}(x_{nchw}-\mu_c(x))^2+ε}\)
- 接下来要把数据进行规范化
- \(\hat{x_i}=\frac{x_i-\mu_c(x_i)}{\sqrt{\sigma_c(x)^2+\epsilon}}\)
- 可以加上扩展和平移参数
- \(y_i=\lambda\hat{x_i}+\beta\)
类比为一摞书,这摞书总共有 N 本,每本有 C 页,每页有 H 行,每行 W 个字符。BN 求均值时,相当于把这些书按页码一一对应地加起来(例如第1本书第36页,第2本书第36页......),再除以每个页码下的字符总数:N×H×W,因此可以把 BN 看成求“平均书”的操作(注意这个“平均书”每页只有一个字),求标准差时也是同理。
一般来说,BN层要放在全连接层或者卷积层后面和非线性映射函数的前面
pytorch实现
```python torch.nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True) torch.nn.BatchNorm3d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
- num_features:一般输入参数为batch_sizenum_features的height*width,即为其中特征的数量,即为输入BN层的通道数;
- eps:分母中添加的一个值,目的是为了计算的稳定性,默认为:1e-5,避免分母为0;
- momentum:一个用于运行过程中均值和方差的一个估计参数(我的理解是一个稳定系数,类似于SGD中的momentum的系数);
- affine:当设为true时,会给定可以学习的系数矩阵gamma和beta
- track_running_stats=True表示跟踪整个训练过程中的batch的统计特性,得到方差和均值,而不只是仅仅依赖与当前输入的batch的统计特性。相反的,如果track_running_stats=False那么就只是计算当前输入的batch的统计特性中的均值和方差了。当在推理阶段的时候,如果track_running_stats=False,此时如果batch_size比较小,那么其统计特性就会和全局统计特性有着较大偏差,可能导致糟糕的效果。
- Layer Normalization
- BN 的一个缺点是需要较大的 batchsize 才能合理估训练数据的均值和方差,这导致内存很可能不够用,同时它也很难应用在训练数据长度不同的 RNN 模型上。Layer Normalization (LN) 的一个优势是不需要批训练,在单条数据内部就能归一化。
- Feature-Map:$x\in R^{N*C*H*W}$
- LN保留了N维度,在每一条数据上进行求平均
- $\mu_n(x)=\frac{1}{CHW}\sum_{c=1}^{C}\sum_{h=1}^{H}\sum_{w=1}^Wx_{nchw}$
- $\sigma_n(x)=\sqrt{\frac{1}{CHW}\sum_c\sum_h\sum_{w}(x_{nchw}-\mu_n(x))^2+ε}$
- 继续采用上一节的类比,把一个 batch 的 feature 类比为一摞书。**LN 求均值时,相当于把每一本书的所有字加起来,再除以这本书的字符总数:C×H×W,即求整本书的“平均字”,求标准差时也是同理**
- pytorch实现
- ```python
torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True)normalized_shape: 输入尺寸
1
[∗×normalized_shape[0]×normalized_shape[1]×…×normalized_shape[−1]]
eps: 为保证数值稳定性(分母不能趋近或取0),给分母加上的值。默认为1e-5。
elementwise_affine: 布尔值,当设为true,给该层添加可学习的仿射变换参数。
Instance Normalization
Instance Normalization (IN) 最初用于图像的风格迁移。作者发现,在生成模型中, feature map 的各个 channel 的均值和方差会影响到最终生成图像的风格,因此可以先把图像在 channel 层面归一化,然后再用目标风格图片对应 channel 的均值和标准差“去归一化”,以期获得目标图片的风格。IN 操作也在单个样本内部进行,不依赖 batch。
Feature-Map:\(x\in R^{N*C*H*W}\)
IN保留了N、C维度,在每一条数据上进行求平均
- \(\mu_{nc}(x)=\frac{1}{HW}\sum_{h=1}^{H}\sum_{w=1}^Wx_{nchw}\)
- \(\sigma_{nc}(x)=\sqrt{\frac{1}{HW}\sum_h\sum_{w}(x_{nchw}-\mu_{nc}(x))^2+ε}\)
IN 求均值时,相当于把一页书中所有字加起来,再除以该页的总字数:H×W,即求每页书的“平均字”,求标准差时也是同理。
pytorch实现
```python torch.nn.InstanceNorm1d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False) torch.nn.InstanceNorm2d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False) torch.nn.InstanceNorm3d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
- num_features: 来自期望输入的特征数,该期望输入的大小为’batch_size x num_features [x width]’
- eps: 为保证数值稳定性(分母不能趋近或取0),给分母加上的值。默认为1e-5。
- momentum: 动态均值和动态方差所使用的动量。默认为0.1。
- affine: 布尔值,当设为true,给该层添加可学习的仿射变换参数。
- track_running_stats:布尔值,当设为true,记录训练过程中的均值和方差;
- Group Normalization
- Group Normalization (GN) 适用于占用显存比较大的任务,例如图像分割。对这类任务,可能 batchsize 只能是个位数,再大显存就不够用了。而当 batchsize 是个位数时,BN 的表现很差,因为没办法通过几个样本的数据量,来近似总体的均值和标准差。GN 也是独立于 batch 的,它是 LN 和 IN 的折中。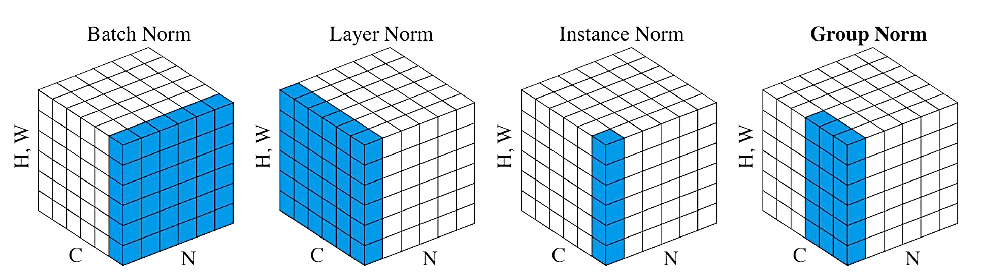
- GN 计算均值和标准差时,把每一个样本 feature map 的 channel 分成 G 组,每组将有$\frac{C}{G}$个channel,然后将这些 channel 中的元素求均值和标准差。各组 channel 用其对应的归一化参数独立地归一化。
- Feature-Map:$x\in R^{N*C*H*W}$
- $\mu_{ng}(x)=\frac{1}{(C/G)HW}\sum_{gC/G}^{(g+1)C/G}\sum_{h=1}^{H}\sum_{w=1}^Wx_{nchw}$
- $\sigma_{ng}(x)=\sqrt{\frac{1}{(C/G)HW}\sum_{gC/G}^{(g+1)C/G}\sum_h\sum_{w}(x_{nchw}-\mu_{ng}(x))^2+ε}$
- **GN 相当于把一本 C 页的书平均分成 G 份,每份成为有 C/G 页的小册子,求每个小册子的“平均字”和字的“标准差”**
- pytorch实现
- ```python
torch.nn.GroupNorm(num_groups, num_features, num_channels, eps=1e-05, affine=True)- num_groups:需要划分为的groups
- num_features: 来自期望输入的特征数,该期望输入的大小为’batch_size x num_features [x width]’
- eps: 为保证数值稳定性(分母不能趋近或取0),给分母加上的值。默认为1e-5。
- momentum: 动态均值和动态方差所使用的动量。默认为0.1。
- affine: 布尔值,当设为true,给该层添加可学习的仿射变换参数。
如果把\(x\in \mathbb{R}^{N \times C \times H \times W}\)类比为一摞书,这摞书总共有 N 本,每本有 C 页,每页有 H 行,每行 W 个字符。计算均值时,
- BN 相当于把这些书按页码一一对应地加起来(例如:第1本书第36页,加第2本书第36页......),再除以每个页码下的字符总数:N×H×W,因此可以把 BN 看成求“平均书”的操作(注意这个“平均书”每页只有一个字)
- LN 相当于把每一本书的所有字加起来,再除以这本书的字符总数:C×H×W,即求整本书的“平均字”
- IN 相当于把一页书中所有字加起来,再除以该页的总字数:H×W,即求每页书的“平均字”
- GN 相当于把一本 C 页的书平均分成 G 份,每份成为有 \(\frac{C}{G}\) 页的小册子,对这个 \(\frac{C}{G}\) 页的小册子,求每个小册子的“平均字”
计算方差同理。 此外,还需要注意它们的映射参数\(\gamma\)和\(\beta\) 的区别:对于 BN,IN,GN, 其\(\gamma\)和\(\beta\)都是维度等于通道数 C 的向量。而对于 LN,其\(\gamma\)和\(\beta\)都是维度等于 normalized_shape 的矩阵。最后,BN 和 IN 可以设置参数:
momentum和track_running_stats来获得在全局数据上更准确的 running mean 和 running std。而 LN 和 GN 只能计算当前 batch 内数据的真实均值和标准差。
Lecture 15
HWN高速神经网络的研究动机:
深度学习网络梯度消失/爆炸问题(Vanishing/Exploding Gradient)
连训练集都无法拟合,当神经网络的深度达到一定程度,用反向传播带来梯度无法传播,参数无法更新。
HWN网络架构:
\(y=H(x,W_H)T(x,W_T)+xC(x,W_C)\)
绕过这个非线性的激活函数,直接把x加权到y
传统网络:
\(y=H(x,W_H)\)
残差的精髓:
- 让网络更加适合模型,一些层如果起负面作用,那么直接使用残差绕开,更容易train。
- T是传输参数,C是Carry参数,我们可以简化C为\(C(x,W_T)=1-T(x,W_T)\)
- \(y=\begin{cases}x,\ if\ T(x,W_T)=0\\H(x,W_H),\ if\ T(w,W_T)=1\end{cases}\)
- \(T(x)=\sigma(W_T \ ^Tx+b_T)\)
DRN残差神经网络的研究动机:
解决网络退化问题,加层数,拟合能力和泛化能力都变差了,这是因为网络退化了。
可能网络只是记住了训练集,并没有学习。浅层神经网络比高层神经网络更好的训练效果。那么我们将低层的特征传到高层,那么效果不会比浅层的差。
Identify Mapping by Shortcut
\(y=\mathcal{F}(x,\{W_i\})+x\)
DRN解决梯度消失问题
DRN和之前的HWN一样也可以解决梯度消失问题,因为有一个x加过来了。
数学证明:通过改变模型输出值的构成在梯度计算时融入加法,使得当个别梯度计算即使部分项过小,信息传播也不会消失,解决体度消失问题。
DenseNet
HWN和DRN通过恒等映射,缓解梯度消失和模型退化问题
Dense Net采用的思路是"与其多次学习冗余特征,特征复用,每一层的输入来自前面所有层的输出"
多尺度映射:
- \(x_l=H_l([x_0,x_1,...,x_{l-1}])\)
比较:
- 普通网络:\(x_l=H_l(x_{l-1})\)
- 残差网络:\(x_l=H_l(x_{l-1})+x_{l-1}\)
Lecture 16
[BERT][https://zhuanlan.zhihu.com/p/98855346]
预训练模型
什么是预训练模型:预训练模型主要基于迁移学习,通过从多个原任务中获取重要的知识,再应用到目标任务中
BERT是transformer的一个encoder
- Pre-train:无监督学习
- 重构:使用表征重构词
- Fine-tuned:有监督训练任务层
Pre-Train+Fine-tuned:
使用Model1-BERT作为黑箱,从token开始输入,输出我们只取token的输出(global),作为Model2的输入。
如何得到BERT模型?
Pre-Train
Bert中使用的技巧,Bert和Transformer的Encoder类似。
BERT:双向Transformer的Encoder,通过给定的预料生成每个词语对应的Embedding向量。
BERT的思想
BERT如此成功的一个原因之一是它是基于上下文(context-based)的嵌入模型,不像其他流行的嵌入模型,比如word2vec,是上下文无关的(context-free)。
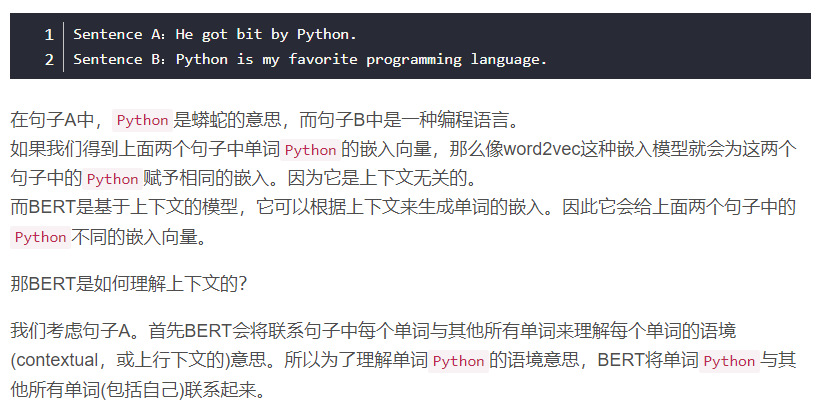
BERT的原理

BERT输入
- Token Embedding
- Position Embedding
- Segment Embedding:表示输入词是第几个句子的
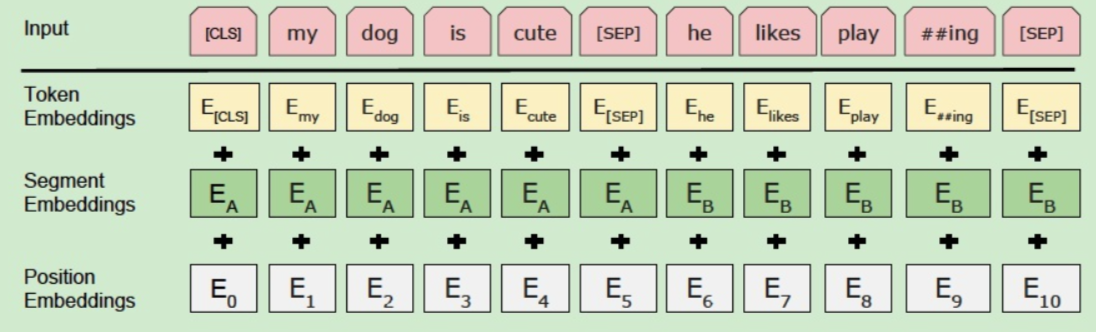
- 我们增加一个新的标记,叫作
[CLS]标记,到第一个句子前面 - 增加一个新的标记,叫作
[SEP]标记,到每个句子的结尾 - 注意
[CLS]标记只加在第一个句子前面,而[SEP]标记加到每个句子末尾。 [CLS]标记用于分类任务,而[SEP]标记用于表示每个句子的结尾。
Fine-Tunning
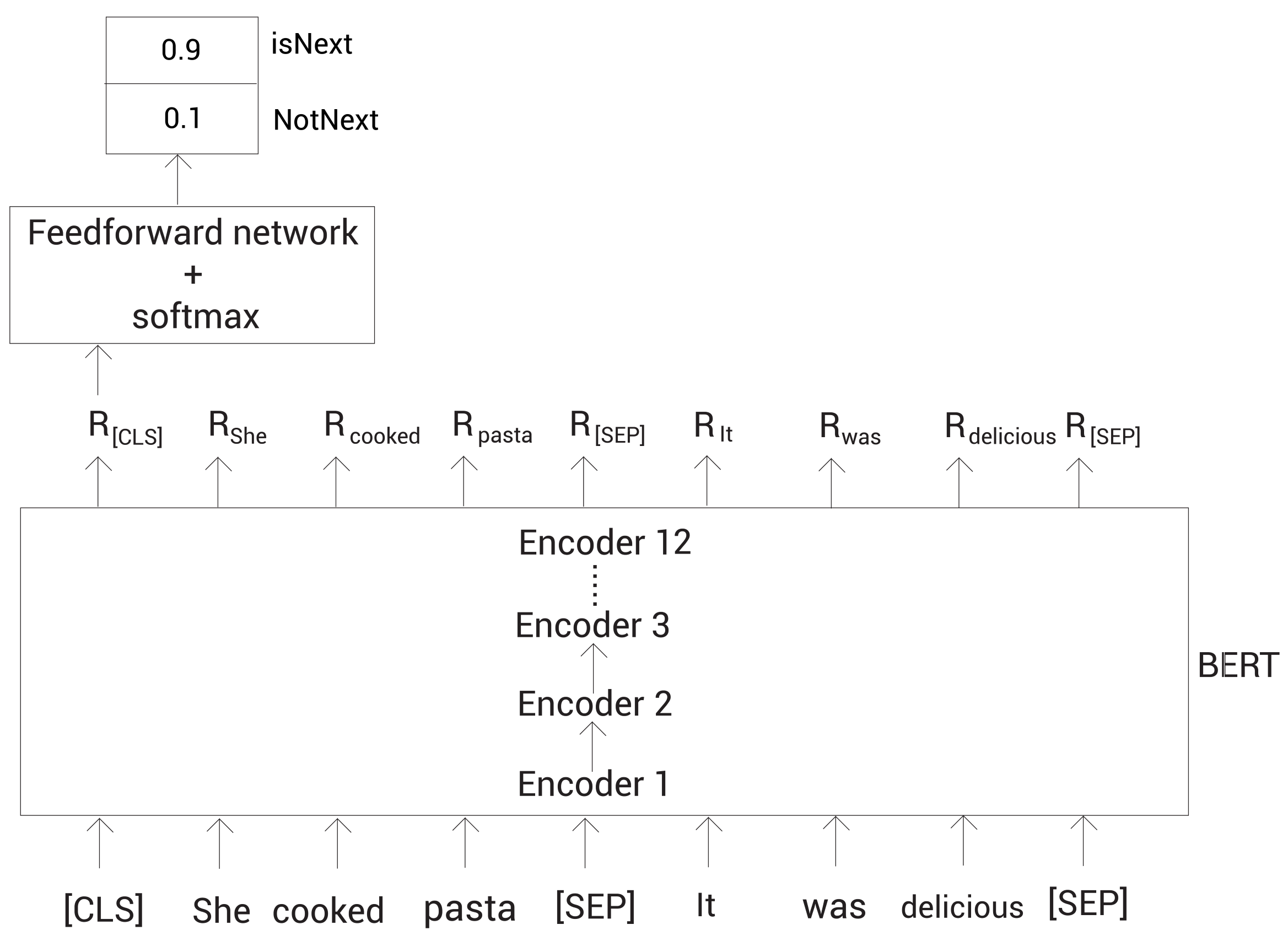
对于Sequence-level的分类任务,BERT可以直接取第一个[CLS]token的final hidden state \(C\in R^H\),加一层权重\(W\in R^{K*H}\),softmax预测\(P=softmax(CW^T)\)
BERT预训练
屏蔽语言建模
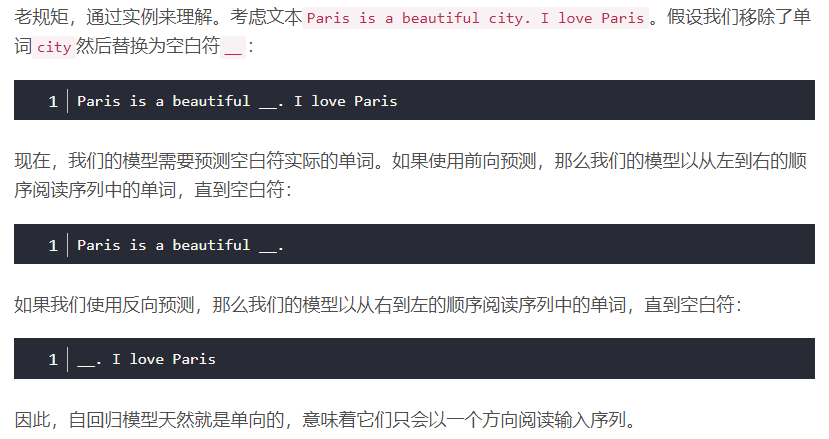
语言建模:训练模型给定一系列单词来预测下一个单词
自回归语言建模
- 前向预测(左到右)
- 反向预测(右到左)
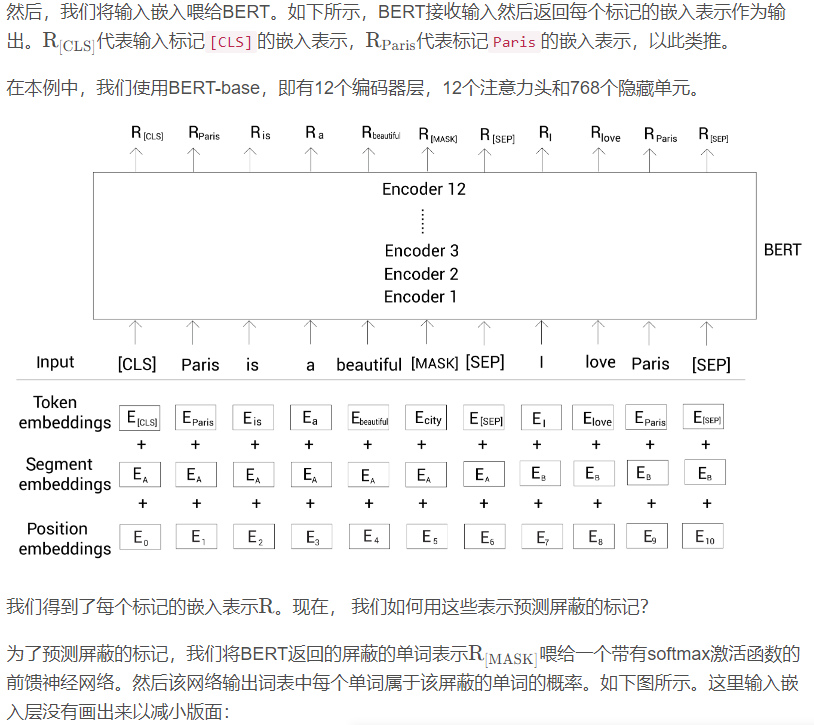
自编码语言建模

BERT是一个自编码语言模型,对于给定的输入序列我们随机屏蔽15%的单词,训练模型去预测这些屏蔽的单词,我们的模型以两个方向读入序列然后尝试预测屏蔽的单词。
掩码序列构建:


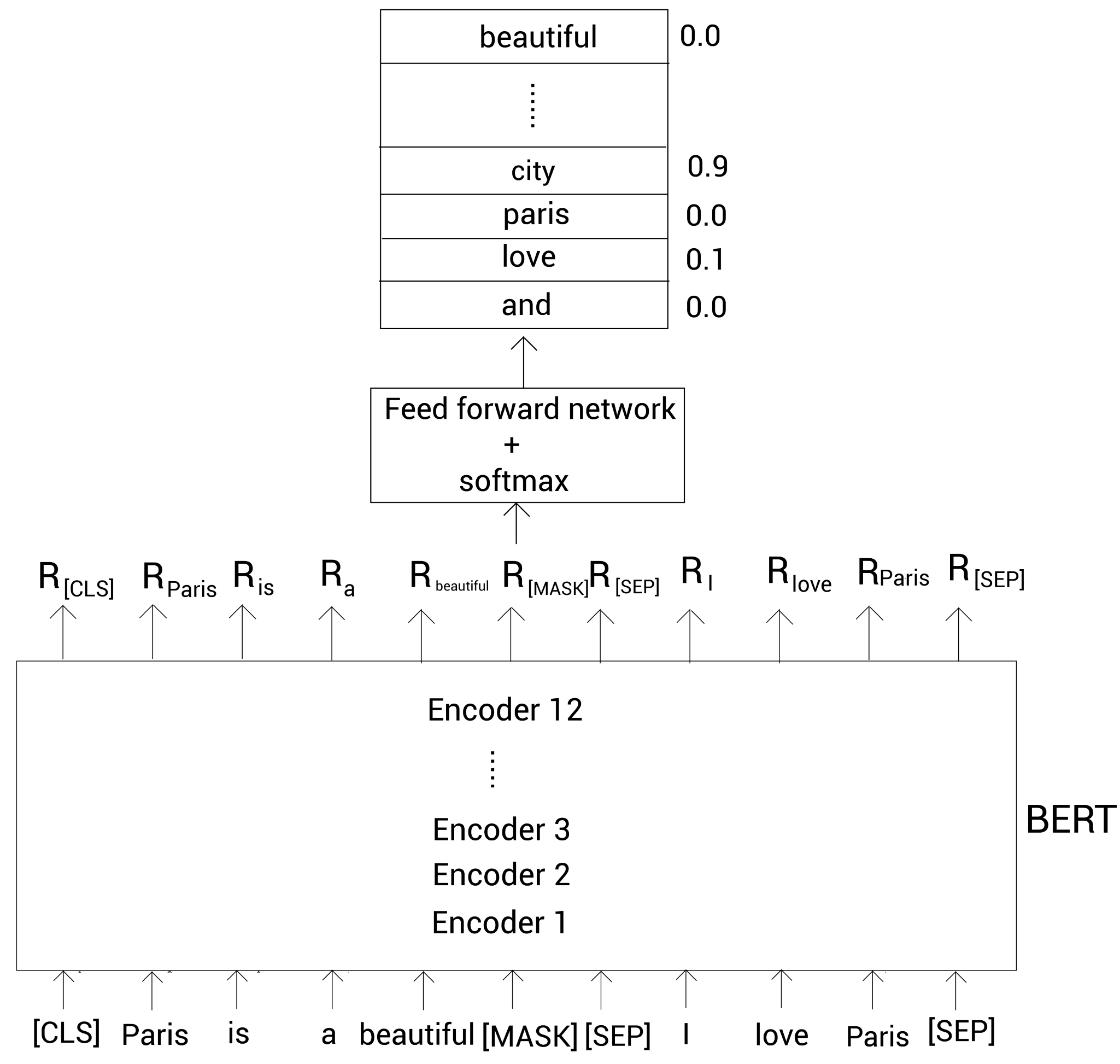

下一句预测NSP
下一句预测(next sentence prediction,NSP)是另一个用于训练BERT模型的任务。NSP是二分类任务,在此任务中,我们输入两个句子两个BERT,然后BERT需要判断第二个句子是否为第一个句子的下一句。
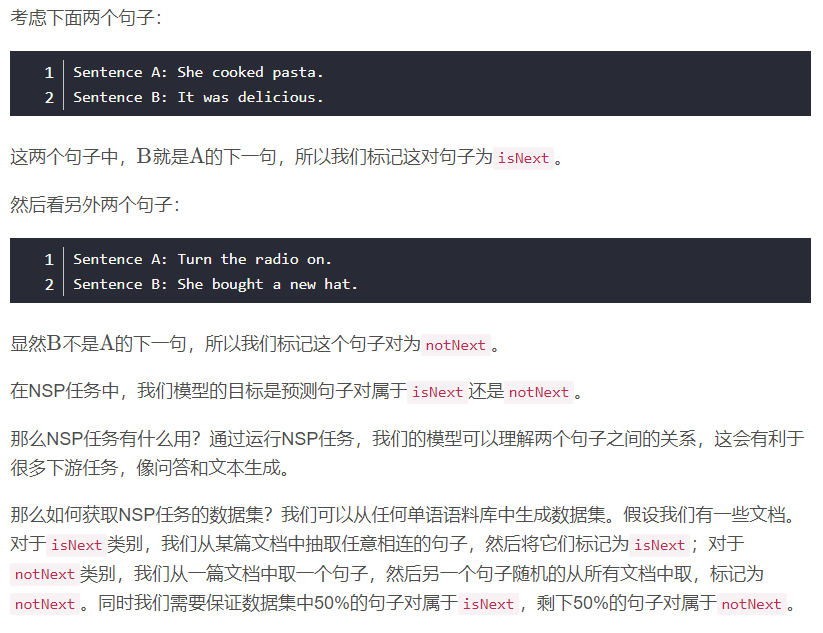



【引用】[原文][https://blog.csdn.net/yjw123456/article/details/120211601]
Lecture 17
预训练模型Ⅱ
CLIP的研究动机
- CLIP解决传统监督与训练模型的高标注和泛化弱的问题。
- 高标注:需要人给数据打标签。
- 泛化弱:不仅要求在训练集上拟合,在测试数据集也要好。
- 互联网上存在大量图像文本对,且样本本身差异性大,不仅解决数据高标注,且容易获得泛化能力强模型。
CLIP模型训练
- load到GPU只能是一个batch的图片和文本对,比如我们load了n个图像文本对
- \(I_i·T_i\)进行关联,大部分的图片和文本是相关联的
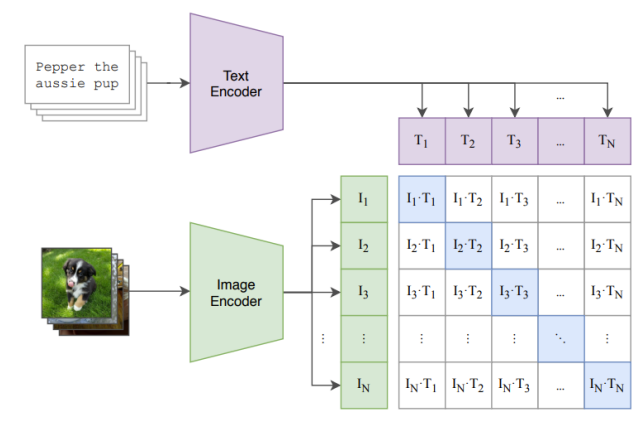
- 我们获得了对角线的正样本。不在对角线的就是负样本。
- 优化目标:\(min(\sum_{i=1}^N\sum_{j=1}^N(I_i·T_j)_{i\neq
j}-\sum_{i=1}^N (I_i·T_i))\)
- 即最大化对角线的值,最小化其他值
CLIP模型分类
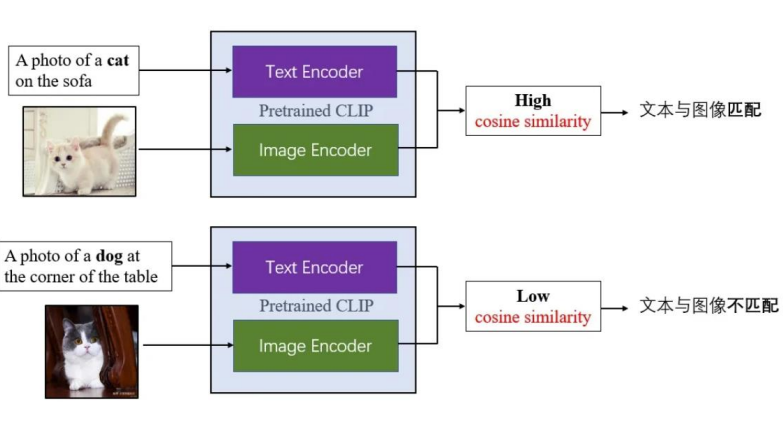
输出的是一个cosine similarity,输入中的文本的黑体部分不仅仅是输入也是分类的一个类。我们可以把CLIP用作分类。将CLIP模型迁移到分类
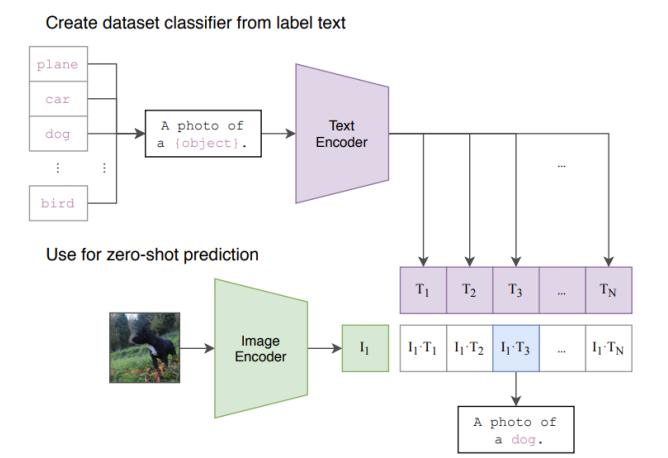
模板模式:输入文本是一个模板,输入的object可以是标签,将待分类的标签转化为句子,进入CLIP,与图片进行比较计算,从标签中获得相似度最大的标签,就是分类。
CLIP模型分类例子
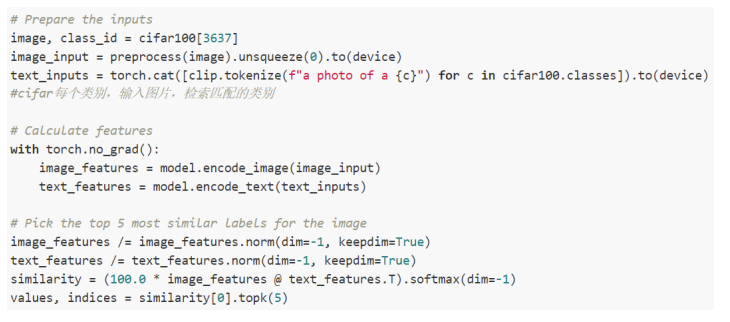
ALIGN的研究动机
示例图像-文本对从ALIGN的训练数据集中随机抽样。一个明显有噪声的文本注释用斜体标记。

- 多模态检索
- 细粒度检索
FILIP的研究动机
CLIP是基于个模态的全局特征间的相似度进行建模的。但是文本和句子距离近是因为有局部特征相似度很高,而不是句子和图片很近。即文本和句子很相似,是因为有局部的特征高度匹配。
FILIP模型
输入:使用transformer得到图像的patch编码和文本的编码
- 全局特征在第0位,但是我们不用,我们用剩余的n位
- 从数据相似度到了token的相似度。
- 一个句子和一个图片是有关联的:某个patch和某个单词匹配
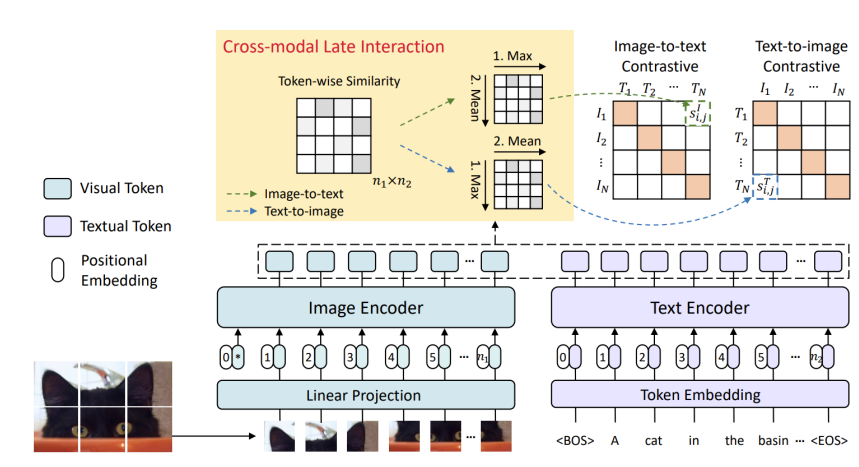
获得:
- 每一对文本图像对获得一个Token-wise Similarity矩阵,这个矩阵可以获得两个矩阵

- 19.51
[数据增强][https://www.zhihu.com/question/319291048]
数据增强也叫数据扩增,意思是在不实质性的增加数据的情况下,让有限的数据产生等价于更多数据的价值。
对数据进行扰动获得新的数据正例。
DECLIP的研究动机
CLIP使用了4亿图像文本对,是否存在较少数据下依旧可以取得不错效果的方法。
能不能使用小的数据集?拉开数据集里面样本的差异性。
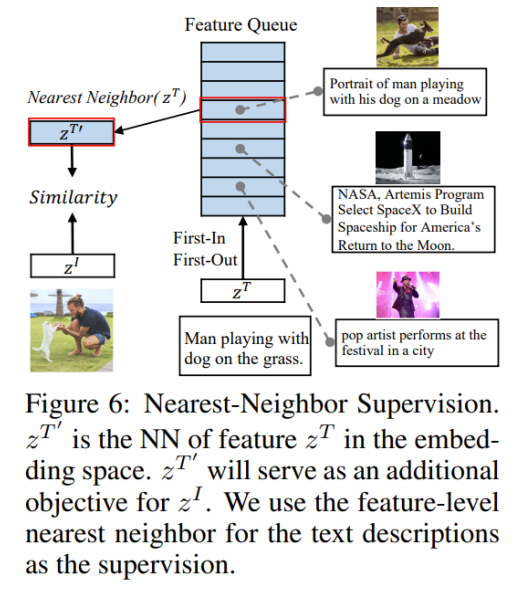
最近邻监督NNS
将最近邻的文本和图片进行重新配对,获得新的文本图片对
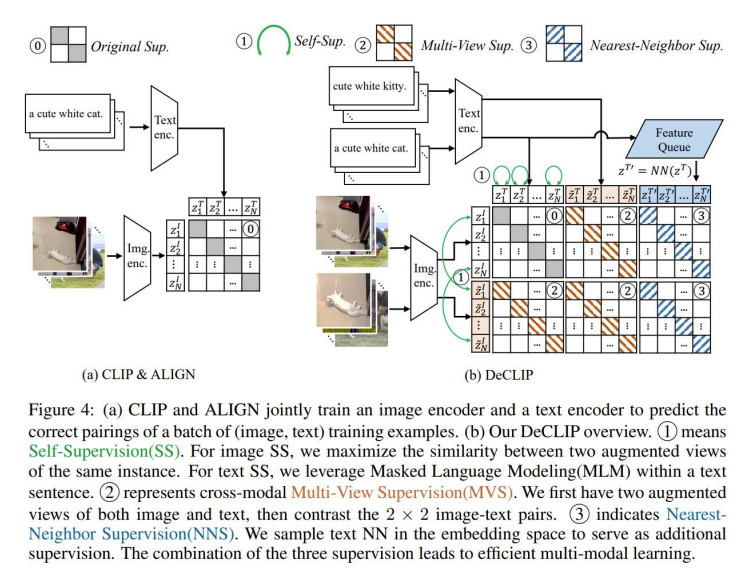
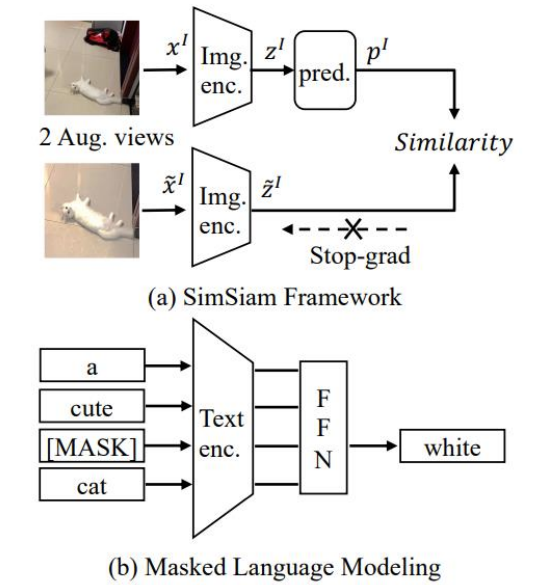
自监督学习
依靠自己创造新的文本图片对,创造正例
Lecture 18
知识蒸馏Distilling Knowledge
知识蒸馏(knowledge distillation)是模型压缩的一种常用的方法,不同于模型压缩中的剪枝和量化,知识蒸馏是通过构建一个轻量化的小模型,利用性能更好的大模型的监督信息,来训练这个小模型,以期达到更好的性能和精度。最早是由Hinton在2015年首次提出并应用在分类任务上面,这个大模型我们称之为teacher(教师模型),小模型我们称之为Student(学生模型)。来自Teacher模型输出的监督信息称之为knowledge(知识),而student学习迁移来自teacher的监督信息的过程称之为Distillation(蒸馏)。
模型背景
训练模型过程中,需要复杂模型和计算资源,从大量与冗余数据中提取信息,因此训练好的模型存在推理速度慢、推理所需资源高的问题。
在模型部署中,对模型推理延迟和计算资源有严格限制。
压缩模型成为机器学习领域的一个问题:在保证性能的前提下减少模型的参数量。
- 一个模型的参数量基本决定了其所能捕获到的数据内蕴含的“知识”量
- 模型参数量与捕获“知识”量之间为边际收益递减的增长。
- 相同模型架构和参数量,训练方法不同,捕获的知识量也不同
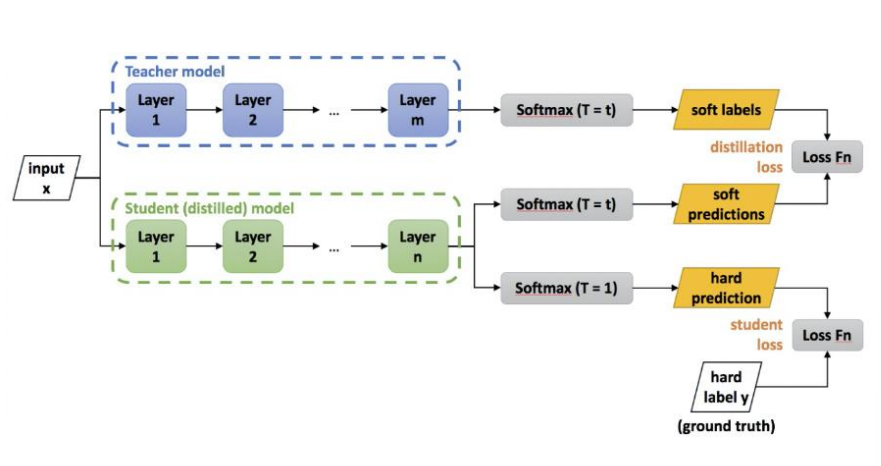
基本框架
模型是“teacher-student”模型。
Teacher模型:原始模型训练,模型复杂,由多个分别训练的模型集成,输出知识。模型参数数量大于学生模型参数数量,可能有多个模型
Student模型:精炼模型训练,参数量少,模型简单的单模型,学习知识
- 传统的学习是直接从数据进行学习,通过数据对,不断减小loss,学习到X到Y的一个映射。
- 知识蒸馏是从教师模型进行学习,教师模型输出知识,学生从知识中学习。
- “Teacher”和“Student”模型满足:对于输入X, 其都能输出Y, Y经过Softmax映射后输出对应类别的概率值
- 学习能力强的“teacher”模型将学习的知识迁移给学习能力弱的“student”模型,增强其泛化能力
- “Teacher”模型扮演导师角色,“student”部署上线
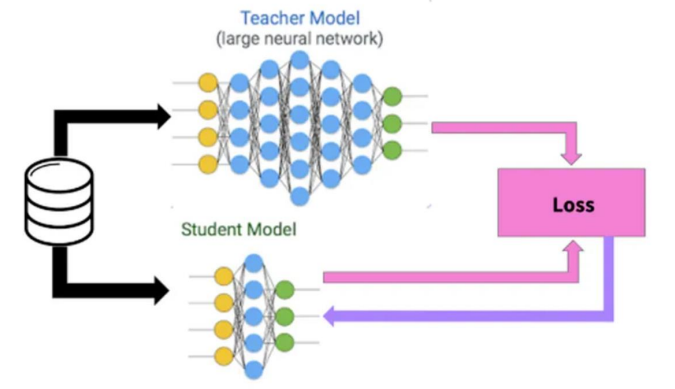
教师模型是已经训练好的,是在云端已经训练好了。并不是让教师学习知识。数据分别进入学生和教师,学生给出答案,校对答案和方法。教师只给一个答案给学生,和直接学习没区别。
目标蒸馏
- 分类问题中模型最后有一个softmax层,其输出值对应相应类别的概率值。
- 传统训练方法通过定义一个损失函数,目标使神经网络预测值 尽可能接近真实值(Hard-target)。
- 与传统训练方法不同,知识蒸馏使用“Teacher”模型的类别概 率作为Soft-target来训练“Student”
- 教师给出的是一个答案的概率(Soft-target)而不是直接一个答案(Hard-target)
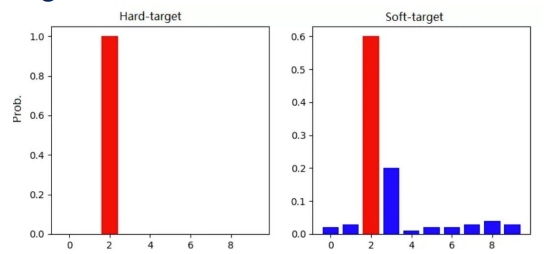
Soft-target训练优势
- 除了正例,负标签也带有“Teacher”模型归纳推理的大量信息 (某负标签对应概率大于其它负标签,代表“Teacher”模型推 理时认为该样本与负标签有一定相似性)。
- 知识蒸馏使得每个样本给“Student”模型带来的信息大于Hard-target的训练方式。
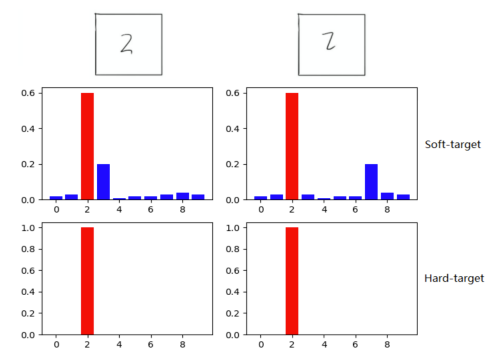
Dark Knowledge暗知识
暗知识:隐藏在深度网络下的网络结构,节点之间的连接权重,以及网络的输出这些看得到的数据下的知识,如上述负标签信息(类别之间关联性的先验信息)。
Training data→big ensemble of learned models→small production model
本质是不仅仅传授明信息,也传授暗知识。
知识如何传授?
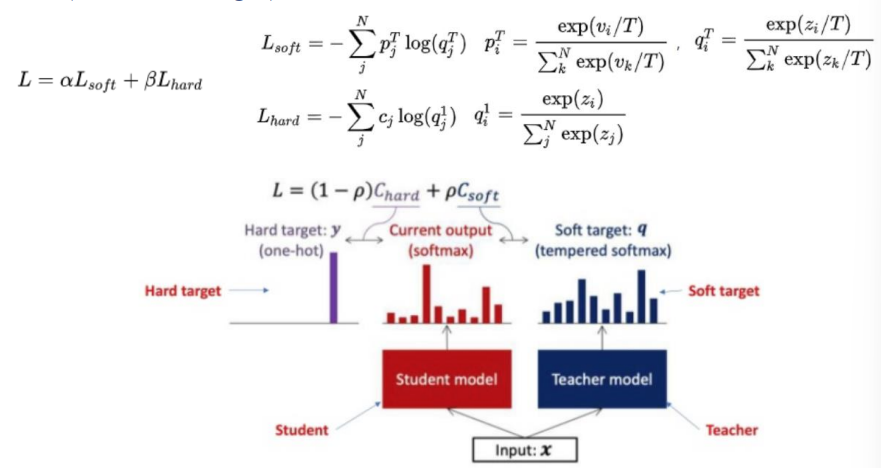
\(q_i=\frac{exp(z_i/T)}{\sum_iexp(z_j/T)}\),zi为标签i输出的概率,教师模型输出分布由T控制
这是一个softmax函数,我们加了一个T,这个T用来控制“温度”。
T越大越陡峭,T越接近0,越平缓。
组合目标优化

Lecture 19
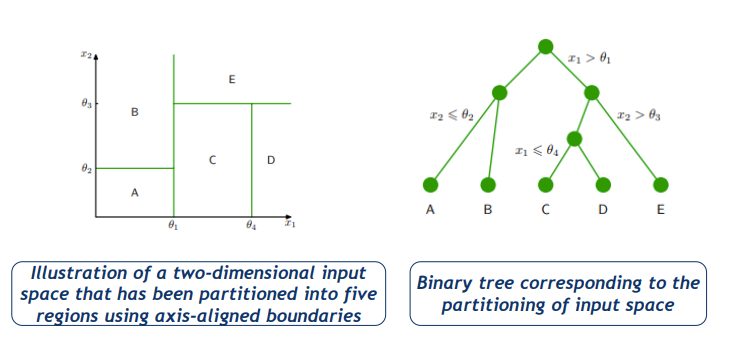
Decision Tree决策树
一种通过实现分而治之策略来表示数据的分层数据结构
- 给定一组例子,学习代表它的决策树。
- 使用这种表示法对新示例进行分类
可以作为一种非参数分类和回归方法。
【Example】
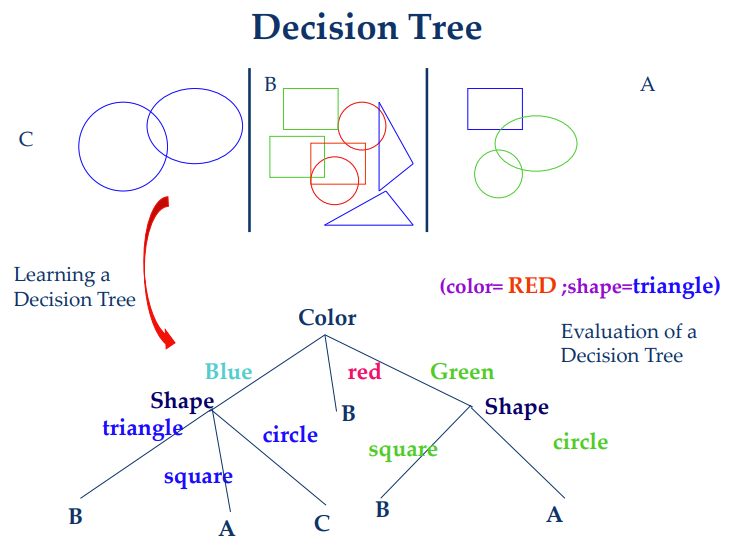
- 决策树是许多的分类器,表示为特征向量
- 节点都是tests for特征值
- 每一个枝条是一种特征值
- 叶节点是一种类别
- 能将实例分类为多个不相关的类别
- 输出是一个离散的类别。实值输出是可能的(回归树)
- 有处理大量数据的有效算法(但没有太多的特征)
- 有处理噪声数据(分类噪声和属性噪声)和处理缺失属性值的方法。
Basic Decision Tree Learning Algorithm
- Data是Batch来的
- 递归构建一个决策树,自顶而下
1 | DT(Examples, Attributes) |
我们希望将示例划分为一个标签中相对纯粹的集合的属性;这样我们就更接近叶节点了。
- 决策树算法中根节点的分类权重最高,向下依次递减;选取分类能力最强的特征作为根节点可以极大的提升分类效率。通过信息增益量化每个特征的分类能力,该特征信息增益越大,分类能力越强,即:计算数据集中各特征点的信息增益,信息增益最大的特征点作为决策树根节点,依次向下递归。
最流行的启发式是基于信息增益的启发式,起源于Quinlan的ID3系统。
Entropy
数据集总体的熵的计算
\(Entropy(S)=-P_+logP_--P_-logP_+\)
- \(P_+\)是集合中正例的百分比
- \(P_-\)是集合中负例的百分比
\(Entropy(S)=-\sum_{i=1}^cP_ilogP_i\)
\(H(D)=-\sum_k^K\frac{|C_k|}{|D|}log_2\frac{|C_k|}{|D|}\)
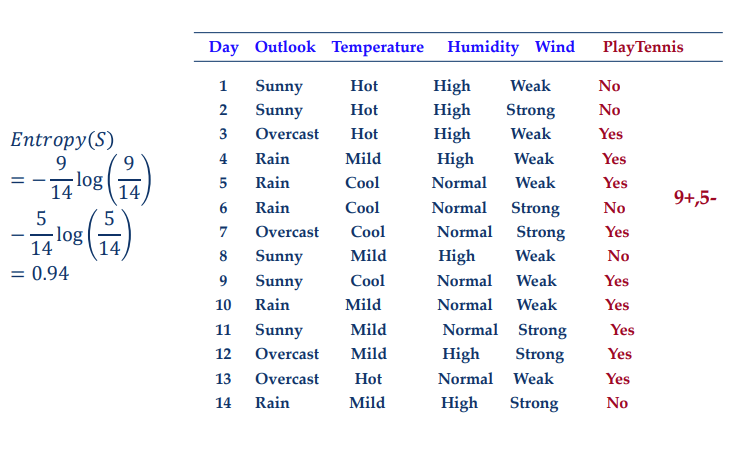
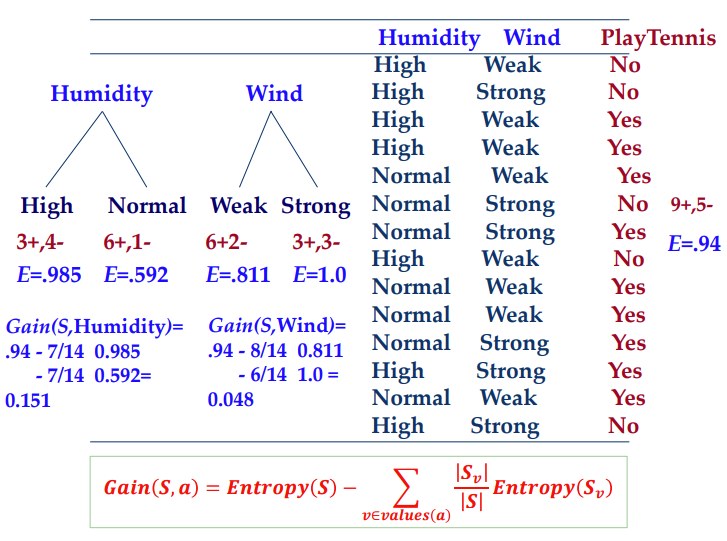
Information Gain
\(Gain(S,a)=Entropy(S)-\sum_{v\in value(a)}\frac{|S_v|}{|S|}Entropy(S_v)\)
特征A对数据集D的熵:
\(H(D|A)=\sum_{v \in value(a)}\frac{|S_v|}{|S|}Entropy(S_v)=\sum_{v \in value(a)}\frac{|S_v|}{|S|}\sum_{k=1}^K\frac{|D_{ik}|}{|D_i|}log_2\frac{|D_{ik}|}{|D_i|}\)
\(g(D,A)=H(D)-H(D|A)\)
总结

Avoid Overfitting
对于决策树:
避免Overfitting可以通过:
- Prepruning:当确定没有足够的数据来做出可靠的选择时,在构建过程中的某个点停止种植树
- Postpruning:生长完整的树,然后删除似乎没有足够证据的节点。
Classification and Regression Trees
ID3存在的问题:
- 只服务于分类
- 特征必须要离散
假设我们有一个回归问题
- 训练数据\(\{x_1,y_1\},...,\{x_n,y_n\}\)
- 一个简单的分类就是划分区域:
- 在每个区域内,都有一个单独的模型来预测目标变量。例如,在回归中,我们可以简单地预测每个区域的常数,或者在分类中,我们可以将每个区域分配给特定的类。
- \(f(x)=\sum_{\tau=1}^Mc_{\tau}I(x\in R_{\tau})\)
- Q 1:
- 什么值我们应该给一个区域赋?
- 我们想要最小均方差
- \(c_{\tau}=\frac{1}{N_{\tau}}\sum_{x_i\in R_\tau}y_i\)
- \(Q_\tau(T)=\sum_{x_i\in R_{\tau}}(y_i-c_\tau)^2\)
- Q 2:
- 如何建立一棵树?
- 即使对于树中固定数量的节点,确定最优结构(包括为每次分裂选择输入变量以及相应的阈值)以最小化平方和误差的问题通常是不可计算的,因为可能的解决方案数量很多。
- 我们使用贪心策略。
- 假设我们对特征\(x^{(j)}\)在值s处分为两个区域
- \(R_1(j,s)=\{x|x^{(j)}\leq s\}\)
- \(R_1(j,s)=\{x|x^{(j)}\gt s\}\)
- 我们选取出使得下式最下的j和s
- \(min_{j,s}[min_{c_1}\sum_{x_i\in R_1(j,s)}(y_i-c_1)^2+min_{c_2}\sum_{x_i\in R_2(j,s)}(y_i-c_2)^2]\)
- 这就是最佳的(j,s)对
- 不短迭代,直到停止
- 假设我们对特征\(x^{(j)}\)在值s处分为两个区域
- 何时停止?
- 假设我们最后有M个区域我们的树表示为
- \(f(x)=\sum_{\tau=1}^Mc_{\tau}I(x\in R_\tau)\)
- 可能的方案:残余误差降低到某个阈值以下
- 然而,它经常被经验发现
- 所有可用的分割都不能显著减少误差
- 经过多次拆分后,发现误差大大减少了。
- 通常的做法是生长一棵大的树,使用基于与叶节点相关的数据点数量的停止准则,然后对生成的树进行修剪。
- 假设我们最后有M个区域我们的树表示为
- 如何剪枝?
- 修剪是基于一个标准,平衡残余误差与模型复杂性的衡量。
- \(f(x)=\sum_{\tau=1}^Mc_{\tau}I(x\in R_\tau)\)
- \(c_{\tau}=\frac{1}{N_{\tau}}\sum_{x_i\in R_\tau}y_i\)
- \(Q_\tau(T)=\sum_{x_i\in R_{\tau}}(y_i-c_\tau)^2\)
- 剪枝准则:
- \(C(T)=\sum_{T=1}^{|T|}Q_\tau(T)+\lambda |T|\)
- 正则化参数\(\lambda\)决定了整体残差平方和误差与以叶节点数目|T|衡量的模型复杂度之间的权衡,其值通过交叉验证选择。
- 修剪是基于一个标准,平衡残余误差与模型复杂性的衡量。
- CART做Classification
- 对于分类问题,我们只使用熵或Gini index,而不是残差平方和:
- \(Q_\tau(T)=-\sum_{k=1}^Kp_{\tau k}log\ p_{\tau k}\)
- \(Q_\tau(T)=\sum_{k=1}^Kp_{\tau k}(1-p_{\tau k})\)
- 当Ptk = 0和Ptk = 1时,它们都消失,并且在Ptk = 0.5时有最大值。它们鼓励形成一个区域,其中高比例的数据点被分配给一个类别。
- 对于分类问题,我们只使用熵或Gini index,而不是残差平方和:
Lecture 20
[组合模型-集成方法][https://zhuanlan.zhihu.com/p/355416998]
Bagging
给定包含m 个样本的数据集,我们先随机取出一个样本放入采样集中,再把该样本放回初始数据集,使得下次采样时该样本仍有可能被选中,这样,经过m次随机采样操作,我们得到含m 个样本的采样集,初始训练集中有的样本在采样集里多次出现,有的则从未出现,初始训练集中约有63.2%的样本出现在来样集中. 照这样,我们可采样出T 个含m 个训练样本的采样集,然后基于每个采样集训练出一个基学习器,再将这些基学习器进行结合.这就是Bagging 的基本流程.在对预测输出进行结合时, Bagging 通常对分类任务使用简单投票法,对回归任务使用简单平均法.若分类预测时出现两个类收到同样票数的情形,则最简单的做法是随机选择一个,也可进一步考察学习器投票的置信度来确定最终胜者.
The Bagging Algorithm
Bagging这个名字来自Bootstrap Aggregating 的缩写[Breiman, 1996d]暗示了的两个关键成分Bagging分为bootstrap和aggregation两种。
- Bootstrap Sampling:从D中统一重新抽样N个样本,并进行替换,也可以使用任意N'来代替原来的N
- Aggregating:采用最流行的策略聚合基础学习者的输出,即投票分类,平均回归。
为什么Bagging Works
- 当基础学习器不稳定(方差大)时,Bagging带来的性能提升较大。
- 基础学习者应该意识到细微的变化,有时允许过拟合。
- 因此,Friedman和Hall[2007]得出结论,Bagging可以减少高阶分量的方差,但不影响线性分量。这意味着Bagging更适用于高度非线性的学习者。
基本思想
- 给定一个弱学习算法,和一个训练集;
- 单个弱学习算法准确率不高;
- 将该学习算法使用多次,得出预测函数序列,进行投票;
- 最后结果准确率将得到提高.
大致过程如下:
- 对于给定的训练样本S,每轮从训练样本S中采用有放回抽样(Booststraping)的方式抽取M个训练样本,共进行n轮,得到了n个样本集合,需要注意的是这里的n个训练集之间是相互独立的。
- 在获取了样本集合之后,每次使用一个样本集合得到一个预测模型,对于n个样本集合来说,我们总共可以得到n个预测模型。
- 如果我们需要解决的是分类问题,那么我们可以对前面得到的n个模型采用投票的方式得到分类的结果,对于回归问题来说,我们可以采用计算模型均值的方法来作为最终预测的结果。
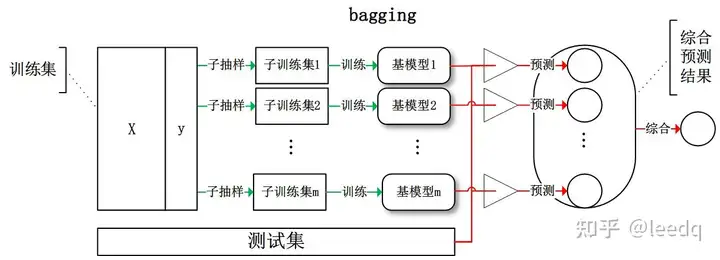
Random Forset
使用决策树作为基模型
选择一个特征子集\(f\subseteq F\)
- 建立决策树:我们选择在f中最优的特征,\(size(f)=\sqrt k\)在分类中,k/3在回归中
- 每一棵树都不如DT,但当它们结合在一起时工作得更好。
构建随机森林,以下步骤进行重复
- 从原始训练中选择一个新的引导样本集
- 建立树
- 在每个内部节点上,从所有特征中随机选择K个特征,然后,在ONLY K个特征中确定最佳分割。
- 不要修剪
- 直到测试误差从未减少(这里指RF中的验证误差)
使得Learners更加Diverse
- 随机森林需要基本的学习者意识到变化很小,有时允许过拟合。
- 每次,基础学习者不是从所有数据中学习,而是从随机引导采样数据中学习。
- 基本的学习者不会使用所有的特征,但随机选择一些特征。
How to Generate M Models
- Bagging
- 使用抽样技术生成不同的训练集
- 每个训练集都可以生成一个模型
- 平行集成法
- Boosting
- 修改不同训练样本的权重
- 在修改后的训练集上生成模型
- 顺序集成法
Boosting
训练后的模型,对训练错误的进行权重增大,接着训练,不断重复。
为了提出一个算法,我们需要回答两个基本问题
- 问题1:如何改变样本的权重,使分类错误的样本得到更多的权重
- 问题2:最后阶段如何结合基础学习者
AdaBoost
- 初始化每一个data的权重\(w_{n}^{(1)}=1/N\)
- 对于任意的m,分类器\(y^{(m)}(x)\)由最小化以下式子而来
- \(J_m=\sum_{n=1}^Nw_n^{(m)}I(y^{(m)}(x_n)\neq t_n)\)
- 评估Errorrate
- \(\epsilon_m=\frac{\sum_{n=1}^Nw_n^{(m)}I(y^{(m)}(x_n)\neq t_n)}{\sum_{n=1}^N w_n^{(m)}}\)
- \(\alpha_m=ln\frac{1-\epsilon_m}{\epsilon_m}\)
- 数据加权系数
- \(w_n^{(m+1)}=w_n^{(m)}exp\{\alpha_mI(y^{(m)}(x_n)\neq t_n)\}\)
- 即分对了不变,分错了更新\(w_n^{(m+1)}=w_n^{(m)}\frac{1-\epsilon_m}{\epsilon_m}\)
- 在指数loss时,更新方式为\(w_n^{(m+1)}=w_n^{(m)}exp\{-\frac{1}{2}t_n\alpha_my_m(x_n)\}\)
- 使用最后的模型进行预测
- 怎么conbine模型?\(\alpha_m\)就是模型m的正确率,正确率高的模型权重大,因此我们进行加权。
- \(Y_M(x)=sign(\sum_{m=1}^M\alpha_my^{(m)}(x))\)
Insights Behing Adaboost
在每一轮中,算法尝试获得不同的基数学习器,从而实现模型的多样性。学习n个分散的模型,消除过拟合,我们需要diverse的模型,不能是相似的。
Adaboost可以看作是指数误差下加性模型的顺序优化过程。
Reweight机制
指数的error function
\(E=\sum_{i=1}^Nexp\{-t_nf_m(x_n)\}\)
其中\(f_m(x)=\frac{1}{2}\sum_{l=1}^m\alpha_l y_l (x)\)
y是预测的值,t是真实值,都是{1,-1}中的。



Gradient Boosting Decision Tree


Lecture 21
K Nearest Neighbor Classifier
KNN:
基本的思想:
- 如果它像鸭子一样走路,像鸭子一样嘎嘎叫,那它很可能就是一只鸭子
- 依然要训练模型,我们要找k个点和它比较相近,我们的模型是这个距离函数
要求三件事:
- 存储记录的集合
- 距离度量来计算记录之间的距离,学习的就是这个
- k的值指的是要检索的最近邻居的数量
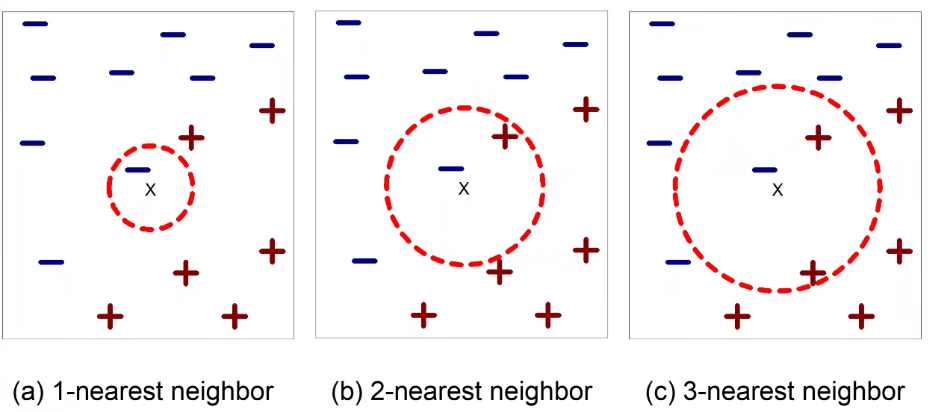
unknow数据点并没有Label,我们要根据学习到的距离函数,检索k个最近的邻居,来估计这个标签
KNN的参数
对于KNN,也有一个决策边界,有N/k个参数。
Metric Learning
如何计算距离?\(ρ(x,y)=\sqrt{(x_1-y_1)^2+...+(x_d-y_d)^2}=\sqrt{(x-y)^T(x-y)}\)
但是这样子有一个问题:不是所有的特征都是一样重要的。我们可以加权。
\(ρ(x,y)=\sqrt{w_1(x_1-y_1)^2+...+w_d(x_d-y_d)^2}\\=\sqrt{(x-y)^T[w^Tw](x-y)}\\=\sqrt{(x-y)^TM(x-y)}\)
我们不知道这个M,我们需要学习这个M
对于\(x和x'\)不是在同一个集合,我们希望他们的距离尽可能大;反之,在同一个集合,我们就希望距离尽可能小。
\(L(M)=\sum_{(x,x')\in S}ρ^2_M(x_i,x_j)-\lambda\ log\sum_{D}ρ_M(x_i,x_j)\)
优化:
- \(min_{M\in R^{d\times d},M\geq 0}\sum_{(x_i,x_j)\in S}ρ^2_M(x_i,x_j)\)
- \(s.t.\ \sum_{(x_i,x_j)\in D}ρ_M(x_i,x_j)\geq 1\)
\(min_{M\geq 0}F(M)=\sum_{(x,x')\in S}ρ^2_M(x_i,x_j)-log(\sum_{(x_i,x_j)\in D}ρ_M(x_i,x_j))\)

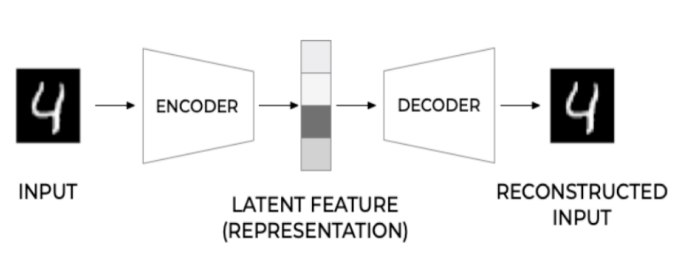
Auto-encoder AE
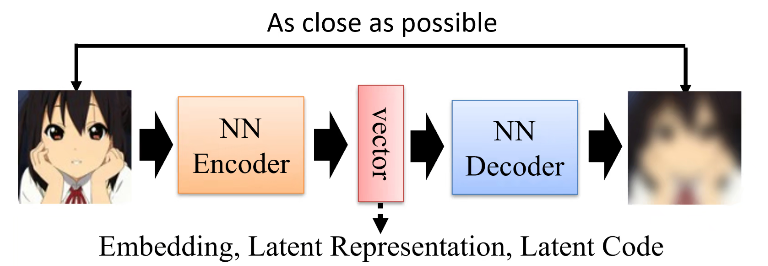
- 高维到低维的投射,再从低维进行重构
- 不仅仅是最小化重构误差
- 更具可解释性的嵌入
Auto Encoder MINIST
28*28的输入,进入NN Encoder,输出一个Code是小于784的,即将高维的投射到了低维的语意空间,是一个表示的问题。
低维表示输入NN Decoder重构高维数据,是一个生成的问题。
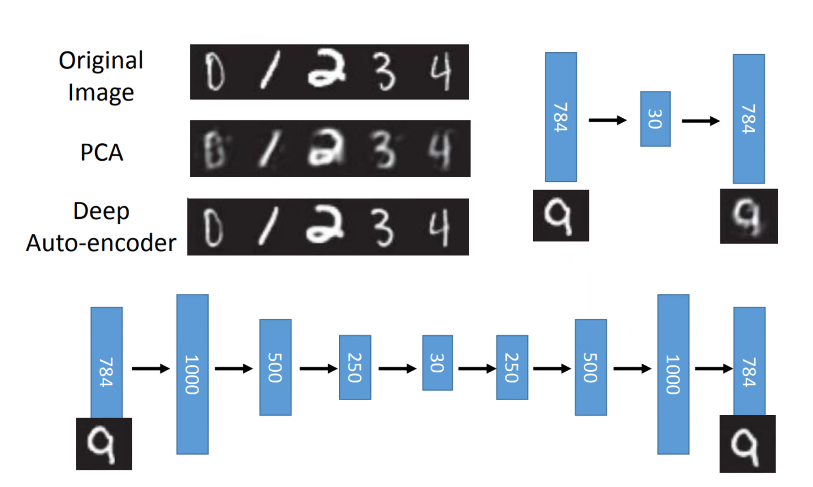
- PCA的降维方法:线性的降维和线性的还原
- 深度的Auto-Encoder
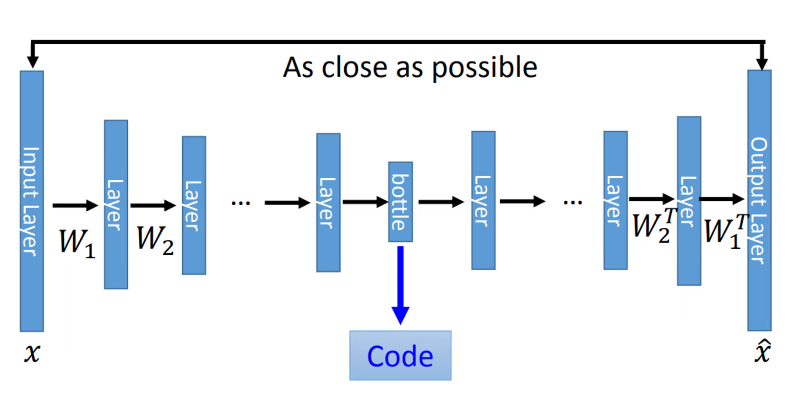
加了很多的层,可以把线性的变成非线性的。
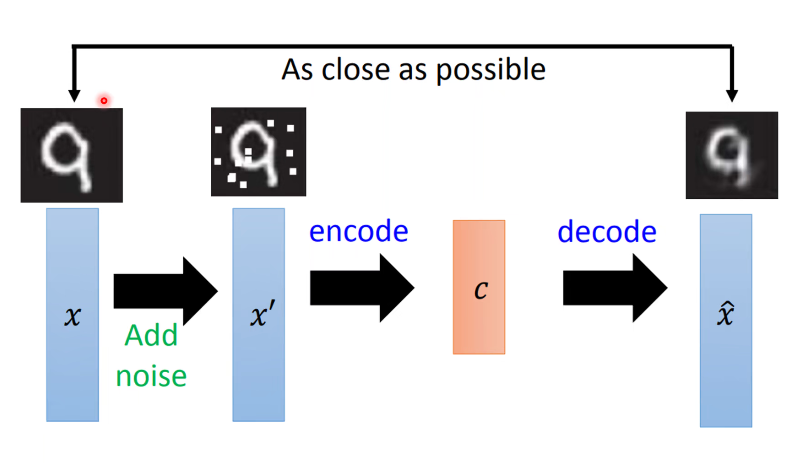
技巧一:去噪Auto-Encoder
不希望从原始输入中提取特征,我们再原始输入可以加入噪声,再进行特征的抽取。编码器可以学习更加鲁棒的特征。
技巧二:基于CNN的Auto-Encoder
将输入进行卷积、池化、激活等,先进行降维再进行特征提取。再进行反卷积、Unpooling等。
Deconvolution:
本质也是一个卷积[参考][https://blog.csdn.net/tfcy694/article/details/89073443]
特征解耦
- 对象包含多个方面的信息
- 我们可以将各个特征进行分离和合成
离散表示VQ-VAE
AE总结
AE是个深度的降维方法,比PCA更好的reconstruction的过程。是PCA的非线性变化。
这是PCA方法:是线性的。
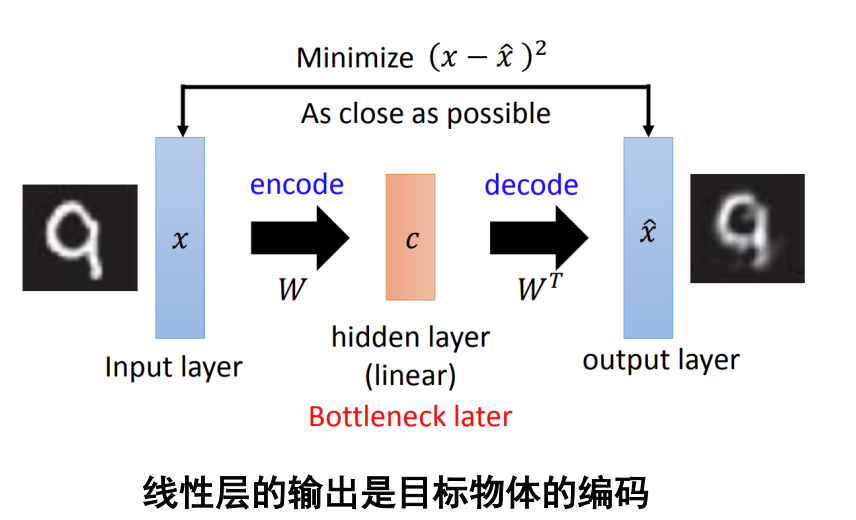
这是AE:网络的每一层是线性的,但是又非线性激活
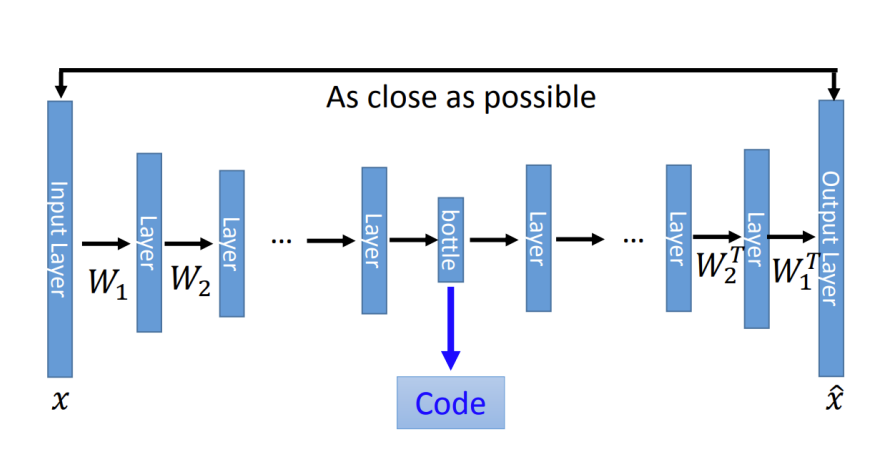
AE的问题:
- AE通过编码器z=g(x),将每个图片编码成向量z,它的解码器f(z)利用编码项链z来重构图片。
- 当AE作为生成模型,针对随机生成的编码向量z,f(z)只会生成没有意义的噪声,因为有些z根本就没有对应的x。
- 原因在于AE没有对z的分布p(z)进行建模,所以不确定哪些z能够生成有用的图片,训练f(z)数据有限,只能对有限的z进行相应。
- 再AE的基础上,显性对z的分布p(z)进行建模,使得自编码器成为一个合格的生成模型VAE
- 两者虽然都是X->Z->X’的结构,但是AE寻找的是单值映射关系,即:z=f(x)。 而VAE寻找的是分布的映射关系,即:DX→DZ
[VAE][https://blog.csdn.net/a312863063/article/details/87953517]
变分自编码器(VAE)解决了自编码器中非正则化潜在空间的问题,并为整个空间提供了生成能力。 AE 中的编码器输出潜在向量。VAE的编码器不输出潜空间中的向量,而是输出每个输入的潜空间中预定义分布的参数。然后VAE对这个潜在分布施加约束,迫使它成为一个正态分布。这个约束确保了潜在空间是正则化的。
其基本思路是很容易理解的:把一堆真实样本通过编码器网络变换成一个理想的数据分布,然后这个数据分布再传递给一个解码器网络,得到一堆生成样本,生成样本与真实样本足够接近的话,就训练出了一个自编码器模型。那VAE(变分自编码器)就是在自编码器模型上做进一步变分处理,使得编码器的输出结果能对应到目标分布的均值和方差,如下图所示:

结构: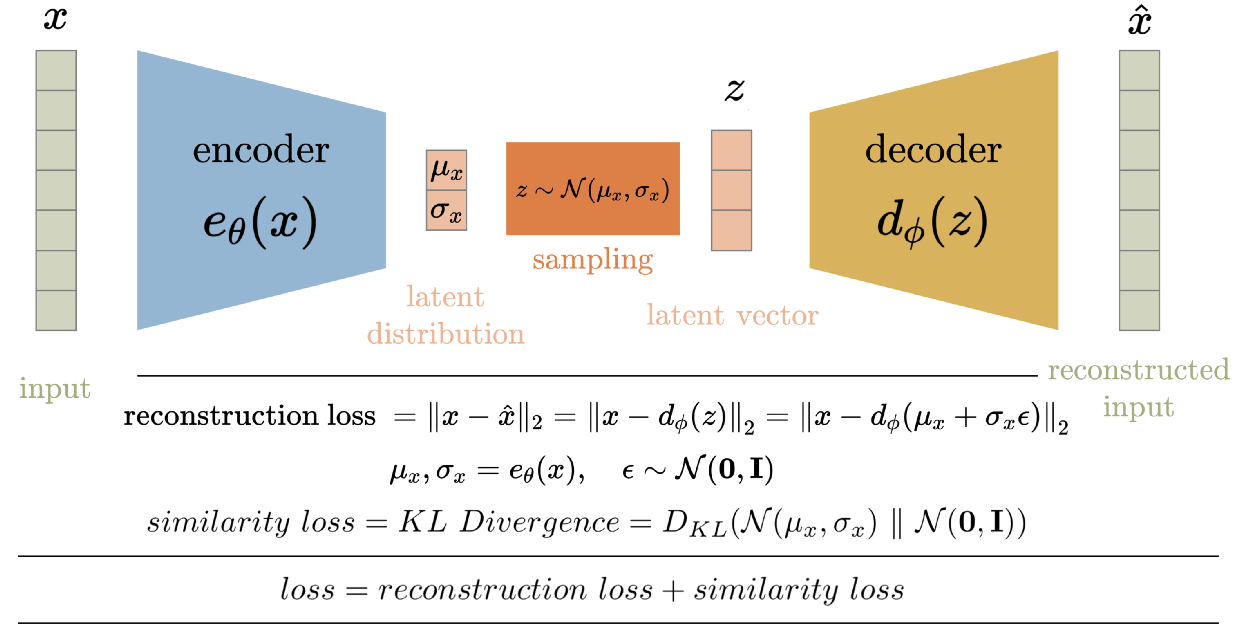
AE是一个向量,一个特征,Latent Representation
VAE是一个高斯分布的两个参数:\(\mu,\sigma\),加入全连接层生成均值和方差,每一个特征都要有一个分布。还原时使用在特征的分布上采样一个点。
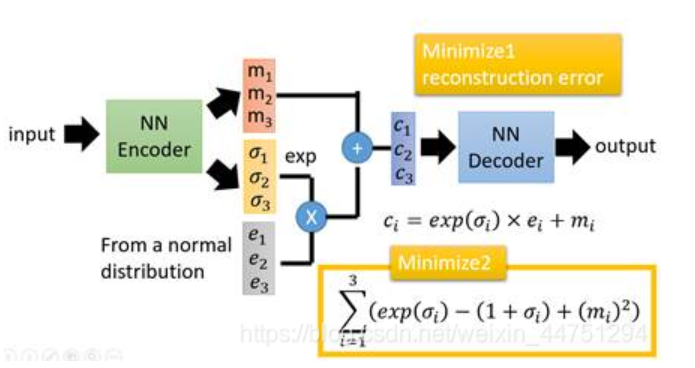
1 | 在auto-encoder中,编码器是直接产生一个编码的,但是在VAE中,为了给编码添加合适的噪音,编码器会输出两个编码,一个是原有编码(m1,m2,m3)【个人觉得和μ1,μ2一样的】,另外一个是控制噪音干扰程度的编码(σ1,σ2,σ3),第二个编码其实很好理解,就是为随机噪音码(e1,e2,e3)分配权重,然后加上exp(σi)的目的是为了保证这个分配的权重是个正值,最后将原编码与噪音编码相加,就得到了VAE在层的输出结果(c1,c2,c3)。其它网络架构都与Deep Auto-encoder无异。 |
VAE数学原理
Encoder
学习\(q_{\phi}(x|z)\)
Decoder
学习\(p_{\theta}(x|z)\)
VAE图结构模型
N是N个data,两个变量的依赖关系:参数\(\theta\),N个z
\(P(x)=\int_z P(x|z)P(z)dz\)
映射函数
- \(X=g(z)\)
- \(g(z)=z/10+z/||z||\)
- 采样高斯模型z可以生成一个x的data的形式。
数据生成
z的空间是一个高斯的分布,P(x)是数据空间。
什么是高斯混合模型呢?就是说,任何一个数据的分布,都可以看作是若干高斯分布的叠加。
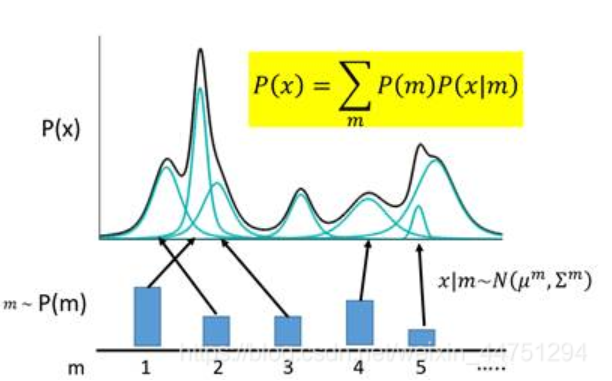
如图所示,如果P(X)代表一种分布的话,存在一种拆分方法能让它表示成图中若干浅蓝色曲线对应的高斯分布的叠加。有意思的是,这种拆分方法已经证明出,当拆分的数量达到512时,其叠加的分布相对于原始分布而言,误差是非常非常小的了。
于是我们可以利用这一理论模型去考虑如何给数据进行编码。一种最直接的思路是,直接用每一组高斯分布的参数作为一个编码值实现编码。
如上图所示,m代表着编码维度上的编号,譬如实现一个512维的编码,m的取值范围就是1,2,3……512。m会服从于一个概率分布P(m)(多项式分布)。现在编码的对应关系是,每采样一个m,其对应到一个小的高斯分布N(μm,∑m),P(X)就可以等价为所有的这些高斯分布的叠加,即:
\(P(x)=\sum_m P(m)P(x|m)\)
\(x|m\)~\(N(\mu^m,\Sigma^m)\)
上述的这种编码方式是非常简单粗暴的,它对应的是我们之前提到的离散的、有大量失真区域的编码方式。于是我们需要对目前的编码方式进行改进,使得它成为连续有效的编码。
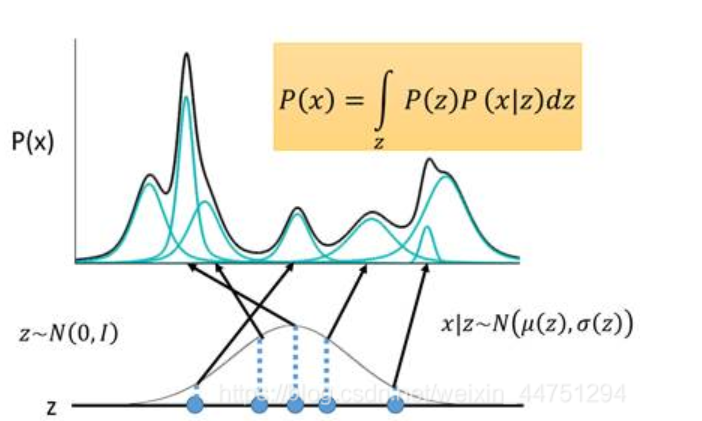
现在我们的编码换成一个连续变量z,我们规定z服从正态分布N(0,1)(实际上并不一定要选N(0,1)用,其他的连续分布都是可行的)。每对于一个采样z,会有两个函数μ和σ,分别决定z对应到的高斯分布的均值和方差,然后在积分域上所有的高斯分布的累加就成为了原始分布P(X)。
\(P(x)=\int_z P(z)P(x|z)dz\)
\(P(x|z)\)~\(N(\mu(z),\sigma(z))\)
- 那么我们知道P(z)是已知的,是一个正态分布
- \(P(x|z)\)是和\(\mu(z),\sigma(z)\)有关的
- 那么P(x)通常是复杂的,因此我们用神经网络计算这个\(\mu,\sigma\)
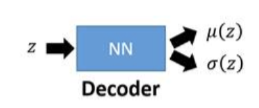
Decoder[关于Decoder和Encoder的理解][https://zhuanlan.zhihu.com/p/55557709]
Decoder做的事情就是计算这个\(\mu(z),\sigma(z)\)
等价于求解\(P(x|z)\),就是求解了\(P(x)\)
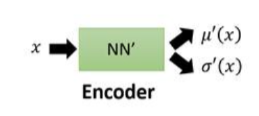
Encoder
Encoder做的事情是求解\(q(z|x)\),q可以是任何分布,将x编码为隐变量z
回到我们要求解的目标式子:
\(P(x)=\int_z P(z)P(x|z)dz\)
我们希望这个P(x)越大越好,就是求解\(log P(x)\)的最大
我们想要最大化P(x)
- \(logP(x)=\int_zq(z|x)logP(x)dz\)
- \(=\int_z q(z|x)log(\frac{P(z,x)}{P(z|x)})dz\)
- \(=\int _zq(z|x)log(\frac{P(z,x)}{q(z|x)}\frac{q(z,x)}{P(z|x)})dz\)
- \(=\int_z q(z|x)log(\frac{P(z,x)}{q(z|x)})dz+\int_z q(z|x)log(\frac{q(z,x)}{P(z|x)})dz\)
- \(=\int_z
q(z|x)log(\frac{P(z,x)}{P(z|x)})dz+D_{KL}(q(z|x)||P(z|x))\)
- 这个第二项是KL散度,是一个非负的值
- \(D_{KL}(p||q)=p(x_i)[log(p(x_i))-log(q(x_i))]\)
那么一个P(x)的下界就有了
\(log(P(x))\geq \int_z q(z|x)log(\frac{P(z,x)}{P(z|x)})dz\)
记作\(L_b=\int_z q(z|x)log(\frac{P(x|z)P(z)}{q(z|x)})dz\)
于是\(logP(x)=L_b+D_{KL}(q(z|x)||P(z|x))\)
VAE的精妙之处来了:
原本,我们要P(x|z)使得\(log P(x)\)最大,现在引入了一个\(q(z|x)\),变成了同时求\(P(x|z),q(z|x)\)使得\(logP(x)\)最大,那么\(L_b,logP(x)\)的关系是什么?
很显然,\(logP(x)\)和\(q(z|x)\)是无关的。
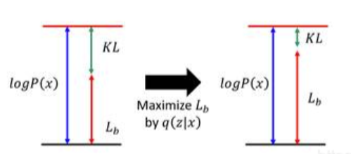
调节这个\(q(z|x)\)可以使得KL散度变小,当\(q(z|x)\)和\(P(z|x)\)一致时,KL散度为0。
同时\(L_b=logP(x)\)。无论这个\(logP(x)\)值如何,我们可以调节使得\(L_b=logP(x)\),又同时正好是下界,最大化\(logP(x)\)我们就直接求\(Max\ L_b\)即可。
调节\(P(x|z)\)就是调节Decoder,调节\(q(z|x)\)解释调节Encoder。VAE的训练逻辑就是Decoder向前一步,Encoder就调节与其一致,并且Decoder无法后退。
那么我们来\(Max\ L_b\)
- \(L_b=\int_z q(z|x)log(\frac{P(z,x)}{q(z|x)})dz\)
- \(=\int_z q(z|x)log(\frac{P(x|z)P(z)}{q(z|x)})dz\)
- \(=\int q(z|x)log(\frac{P(z)}{q(z|x)})+\int q(z|x)logP(x|z)dz\)
- \(=-D_{KL}(q(z|x)||P(z))+\int q(z|x)logP(x|z)dz\)
- 即求解\(D_{KL}(q(z|x)||P(z))\)最小值,\(\int q(z|x)logP(x|z)dz\)最大值
\(D_{KL}(q(z|x)||P(z))\)展开式为\(\sum_{i=1}^J(exp(\sigma_i)-(1+\sigma_i)+m_i^2)\)
\(max\ \int q(z|x)logP(x|z)dz=max\ E_{q(z|x)}[logP(x|z)]\)
这个期望就是一个损失函数。

Lecture 22
VAE Review
- AE:INPUT、ENCODER、LATENT FEATURE、DECODER、RECONSTRUCTED INPUT
- VAE
- \(z_i=\mu_i+\sigma_i·\epsilon _i\),Reparameterization Trick
C-VAE
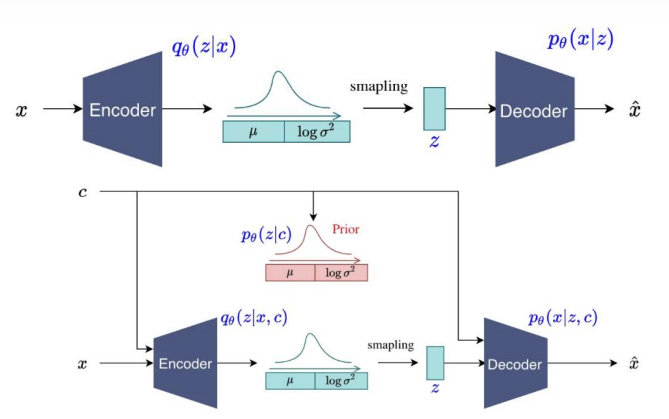

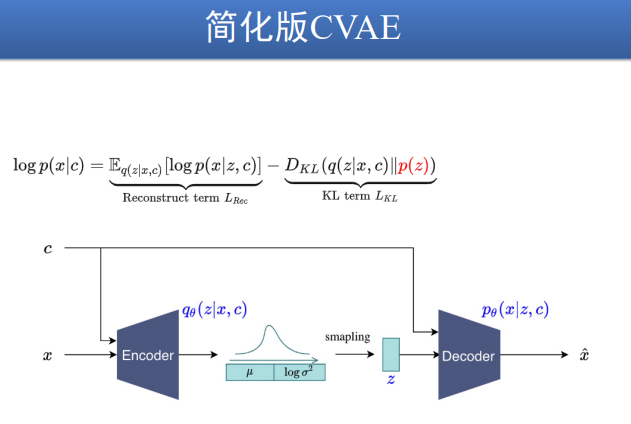
[VQ-VAE][https://zhuanlan.zhihu.com/p/91434658]
VAE和VE的不同之处在与,VAE不再去学习一个连续的表征,而 是直接学习一个分布,然后通过这个分布采样得到中间表征去 重建原图。
VAE使用了固定的正态分布先验,以及连续的中间表征,导致 图片生成的多样性弱和可控性差。
前面看到, VAE的隐变量 z 的每一维都是一个连续的值, 而VQ-VAE最大的特点就是, z的每一维都是离散的整数. 这样做符合一些自然界的模态 (a more natural fit for many of the modalities). 比如Language是a sequence of symbols, 或者reasoning, planning and predictive learning. 因此, VQ-VAE可以successfully model important features that span many dimensions in data space, 比如图片里某个object会覆盖很多pixel, 音频中一个phoneme会持续很多samples/frames, 而不会去学一些特别细节的东西.
将 z 离散化的关键就是VQ, 即vector quatization. 简单来说, 就是要先有一个codebook, 这个codebook是一个embedding table. 我们在这个table中找到和vector最接近(比如欧氏距离最近)的一个embedding, 用这个embedding的index来代表这个vector.
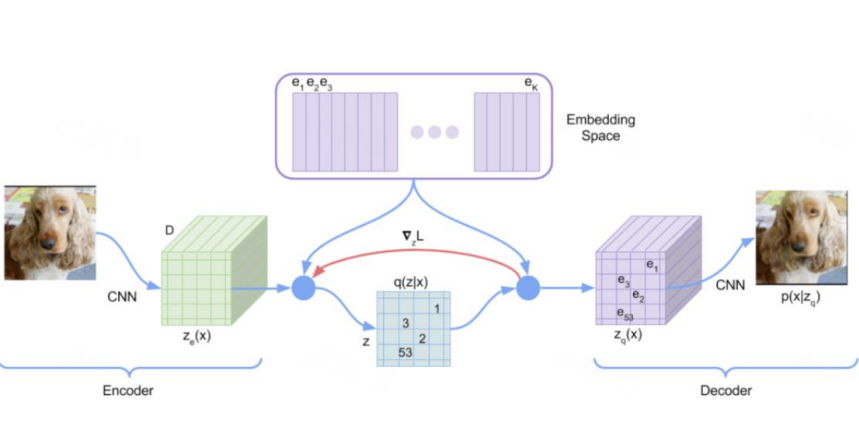
- 自动编码:将input输入,获得Latent Variable,设隐变量的维度为D,输入的size为H *W,则feature map大小为H*W*D
- 降维离散化,学习到一个codebook,codebook中有K个D维度的离散向量\(e_1,...e_K\)
- 最近邻重构,每一个Latent Variable找一个离最近的codebook中的向量\(e_i\),用index i表示,获得了\(q(z|x)\).
- \(z=encoder(x)\)
- \(E=[e_1,e_2,...,e_K]\)
- \(z\rarr e_k,k=argmin_j||z-e_j||^2\)
- \(x\rarr_{encoder}z\rarr_{最近邻}\rarr z_q\rarr_{decoder}\rarr \hat x\)
- 把绿色的\(z_e(x)\) 用codebook里最近的 \(e_i\)替换后可以得到紫色的 \(z_q(x)\) , 这是decoder的输入, 然后reconstruct得到图片.
后验分布\(q(z|x)\)
- 后验分布\(q(z|x)\)是一个多类分布,为one-hot型
- \(q(z=k|x)=\begin{cases}1\ k=argmin_i||z_e(x)-e_i||_2\\0\ otherwise\end{cases}\)
- 基确定分布\(q(z|x)\), 后验分布\(q(z|x)\)和先验分布\(p(z)\)的KL散度为
- \(KL(q(z|x)||p(z))=\sum q(z|x)log\ \frac{q(z|x)}{p(z)}=log\frac{1}{1/K}+0=logK\)
- 给定KL散度为一个常量,VQ-VAE的训练损失项为重建误差 log p(x|z)。
VQ-VAE目标函数
- Reconstruction Loss
- VQ Loss
- commitment loss

其中,reconstruction loss作用在encoder和decoder上,VQ loss用 来更新embedding空间(EMA方式),commitment loss用来约 束encoder。系数beta默认设置为0.25。
Straight-through Estimator
由于argmin操作不可导,重建误差的梯度无法传导到encoder, 采
用straight-through
estimator来采用上游得到的梯度。基于Straight-Through的思想,前项传播的时候可以用想要的变量,而反向传播的时候,用所涉及的梯度。其目标函数为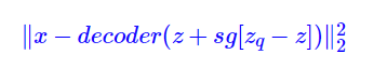
其中,前向传播计算为: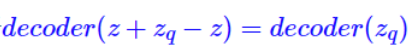
Lecture 23
GAN:Generative Adverasrial Network
- 生成式对抗网络一种深度学习模型,通过生成模型和判别模型进行互相博弈产生相当好的输出。
- 通过对抗过程同时训练两个模型,生成器学会创造看起来真实的图像,鉴别器学会区分生成图片和真实图片。
- 训练期间,生成器变得更好创建看起来真实的图像,鉴别器更好区分它们。当鉴别器不能区分,过程达到平衡。
GAN训练
- 输入一个初始噪声z,然后通过生成器G得到一个伪造的数据G(z)
- 从真实数据中取一部分即真实数据x,将两者混合丢到判别器D,由判别器做这些图像是真是假的二分类,得到概率D(x),计算出loss并且回传。
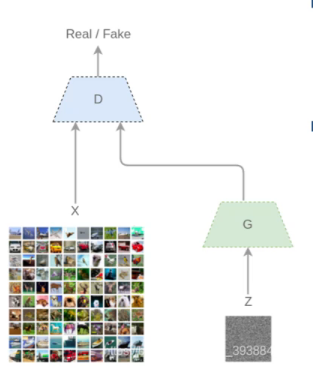
GAN损失价值函数[GAN][https://zhuanlan.zhihu.com/p/34287744]
在训练过程中,生成网络的目标就是尽量生成真实的图片去欺骗判别网络D。而网络D的目标就是尽量把网络G生成的图片和真实的图片分别开来。这样,G和D构成了一个动态的“博弈过程”。这个博弈过程具体是怎么样的呢?
- 根据交叉熵损失的价值函数\(V(D,G)\)
- \(min_Gmax_DV(D,G)=E_{x~p_{data}(x)}[log\ D(x)]+E_{z~p_{z}(z)}[1-log\ D(G(z))]\)
- 其中真实数据的x服从\(p_{data}\)分布,\(p_z(z)\)是噪声z的分布
- \(G(z)\)将z映射到数据空间,拟合真实数据的分布,而D(x)得到真实数据的概率
- 为了学习生成器在数据x上的分布p,训练时自然使D判断x是p中取出的期望E最大化,同时最小化伪造的概率\(log\ ( 1-D(G(z)))\)
- 在这里,训练网络D使得最大概率地分对训练样本的标签(最大化log D(x)和 log(1−D(G(z))) ),训练网络G最小化log(1 – D(G(z))),即最大化D的损失。而训练过程中固定一方,更新另一个网络的参数,交替迭代,使得对方的错误最大化,最终,G 能估测出样本数据的分布,也就是生成的样本更加的真实。
或者我们可以直接理解G网络的loss是\(log(1−D(G(z))\),而D的loss是\(-(log(D(x))+log(1−D(G(z)))\)
- G的训练目标就是让\(D(G(z))\)趋近于1,即让D判别G(z)是正例
- D网络的训练就是一个2分类,目标是分清楚真实数据和生成数据,也就是希望真实数据的\(D(x)\)输出趋近于1,而生成数据的输出即\(D(G(z))\)趋近于0,或是负类。这里就是体现了对抗的思想。
算法层面


Lecture 24
DCGAN
Deep Convolution GAN,判别器是一种ConvNet,接受图像输出预测向量。
ProGAN
渐进式生成的方式是先训练出低分辨率的图片,再逐步增加网络结构提升图片质量。
图片进行下采样,可以获得低分辨率图片从而进行低分辨率的训练。比如我们有1024*1024的图片,我们先下采样获得4*4的图片,进行低分辨率的训练。在逐步增加分辨率。
在加倍分辨率训练的时候,加入平滑转换过程,增加模型训练的稳定程度。
- \(X=X_{16pixel}*(1-\alpha)+X_{32pixel}*\alpha\)
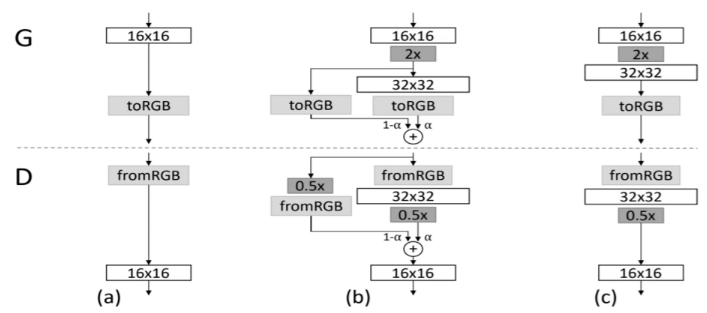
CGAN
生成器和判别器都已额外信息y为条件,GAN模型可以拓展为一个条件模型。
\(min_Dmax_GV(D,G)=E_{x}[logD(x|y)]+E_{z}[log(1-D(G(z|y)))]\)
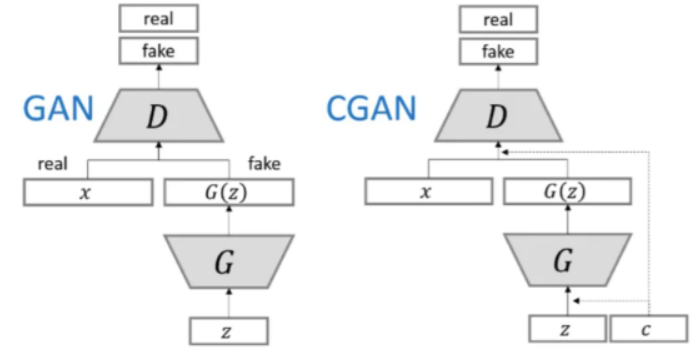
StackGAN
- 什么是StackGAN,怎么提出来的?
- 根据文字描述,人工生成高质量图片的任务是计算机视觉领域一个挑战,并且有很多应用场景。现有的文字转图像方式很难表现文字的含义,并且细节部分缺失严重,不够生动具体。
- 现有的模型(如
Vanilla GAN)只是简单的添加upsampling层来生成高分辨率的图,这会导致训练不稳定,且生成无用的图片 
[StackGAN的模型结构][https://zhuanlan.zhihu.com/p/78102953]
StackGAN是分段式结构
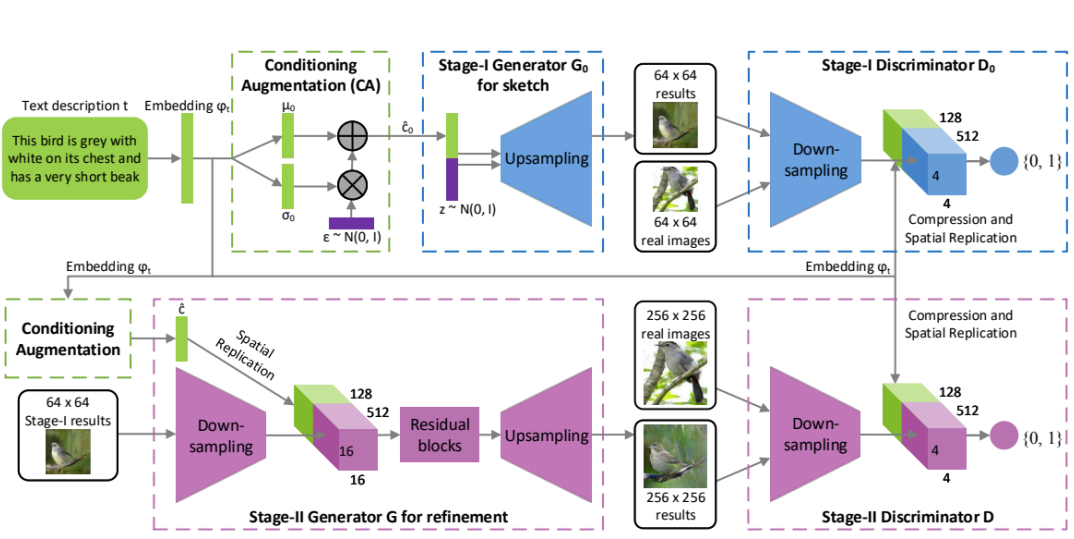
Conditioning Augmentation
根据给定的文字描述,勾勒初始的形状和色彩,生成低分辨率的图像。
TEXT输入,经过pretrained-Text-encoder再经过Embedding获得编码,输入Generator。
描述文字首先被预训练好的编码器编码为词嵌入向量 \(\phi_t\)
在前人的研究中,词嵌入向量被非线性的转换为生成条件隐含变量,并作为生成器的输入。然而,词嵌入的隐含空间维度维度一般很高(> 100)。当输入数据量很少的时候,通常会导致隐含变量分布空间不连续(大部分值为 0,太过稀疏),这对生成器的训练不利。
因此,我们引入条件增强
(Conditioning Augmentation)来产生额外的条件变量 \(\hat c\) 。我们不是选定固定的\(\hat c\) ,而是从独立高斯分布\(N(\mu(\phi_t),\Sigma(\phi_t))\)中随机采样。其中,均值 \(\mu(\phi_t)\) 和对角方差矩阵\(\Sigma(\phi_t)\)是关于词嵌入向量\(\phi_t\)的函数(全连接层子网络)。上面一段话,换言之就是,将原始词向量分布映射到一个高斯分布中,均值和方差不变。给定较少的
text-image对,通过该手段,也能够生成更多的训练样本,并且对于条件空间的微小扰动,其稳健型也更好。为了进一步增强条件分布的平滑性,以及避免过拟合(引入噪声相当于数据增强),我们使用KL散度对其正则化- \(D_{KL}(N(\mu(\phi_t),\Sigma(\phi_t))||N(0,I))\)
Stage-1
第一阶段主要用于生成粗略的形状和颜色等。先从\(N(\mu(\phi_t),\Sigma(\phi_t))\)中随机采样出
\(\hat c_0\) ,并随机采样的高斯噪声
z,将它们进行 concatenate ,然后作为
Stage-I 的输入,来训练判别器 \(D_0\) 和 生成器\(G_0\) ,分别对应如下目标函数:
- \(max L_{D_0}=E_{(I_0,t)~p_{data}}[log(D_0(I_0,\phi_t))]+E_{z~p_z,t~p_{data}}[log(1-D_0(G_0(z,\hat c_0),\phi_t))]\)
- \(min L_{G_0}=E_{z~p_z,t~p_{data}}[log(1-D_0(G_0(z,\hat c_0),\phi_t))]+D_{KL}(N(\mu(\phi_t),\Sigma(\phi_t))||N(0,I))\)
- 其中,真实图像\(I_0\)和文本描述\(t\)源自于实际数据分布\(p_{data}\) 。 \(z\)表示从高斯分布分布\(p_{data}\) 中随机提取的噪声向量。 λ 为正则化参数,用于平衡公式中的两项。
- 其中, \(μ_0(φ_t),Σ_0(φ_t)\) 是与网络剩余部分一起学习
Stage-2
Stage-1
阶段生成的低分辨率图像通常缺乏鲜明的目标特征,并且可能包含一些变形。同时,文本描述中的部分信息可能也未体现出来。所以,通过
Stage-2 可以在 Stage-1
生成的低分辨率图像和文本描述的基础上,生成高分辨率图片,其修正了
Stage-1的缺陷,并完善了被忽略的文本信息细节。
Stage-2 以高斯隐含变量\(\hat
c\)以及 Stage-1 的生成器的输出 \(s_0=G_0(z,\hat c_0)\) 为输入,来训练生成器
G 和判别器 D,其目标函数分别为:
- \(max
L_{D}=E_{(I,t)~p_{data}}[log(D(I,\phi_t))]+E_{s_0~p_{G_0},t~p_{data}}[log(1-D(G(s,\hat
c),\phi_t))]\)
- \(min L_{G}=E_{s_0~p_{G_0},t~p_{data}}[log(1-D(G(s_0,\hat c),\phi_t))]+D_{KL}(N(\mu(\phi_t),\Sigma(\phi_t))||N(0,I))\)
Pix2PixGAN
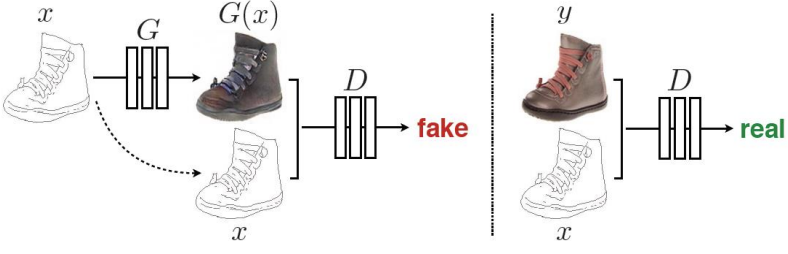
U-Net
U-Net是编码解码结构,编码负责特征提取,解码负责恢复原 始分辨率(上采样和拼接操作)
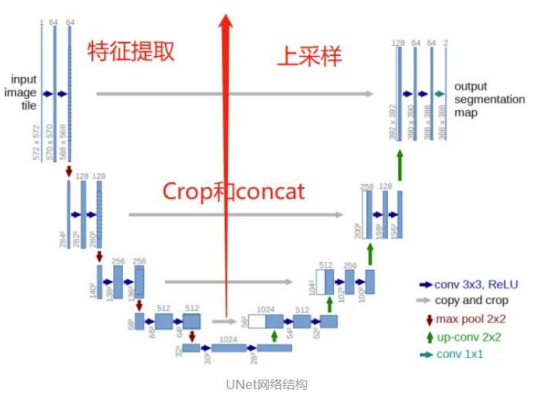
\(L_{cGAN}(G,D)=E_{x,y}[log\ D(x,y)]+E_{x,z}[log(1-D(x,G(x,z)))]\)
\(L_{L_1(G)}=E_{x,y,z}[||y-G(x,z)||_1]\)
\(G^*=argmin_Gmax_DL_{cGAN}(G,D)+\lambda L_{L_1}(G)\)
CycleGAN
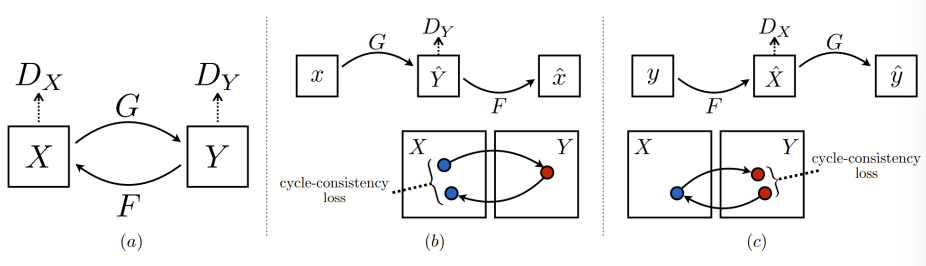
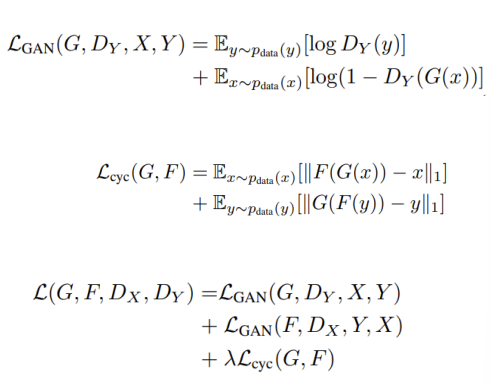
StyleGAN
Lecture 25
[Diffusion Model][https://zhuanlan.zhihu.com/p/525106459]
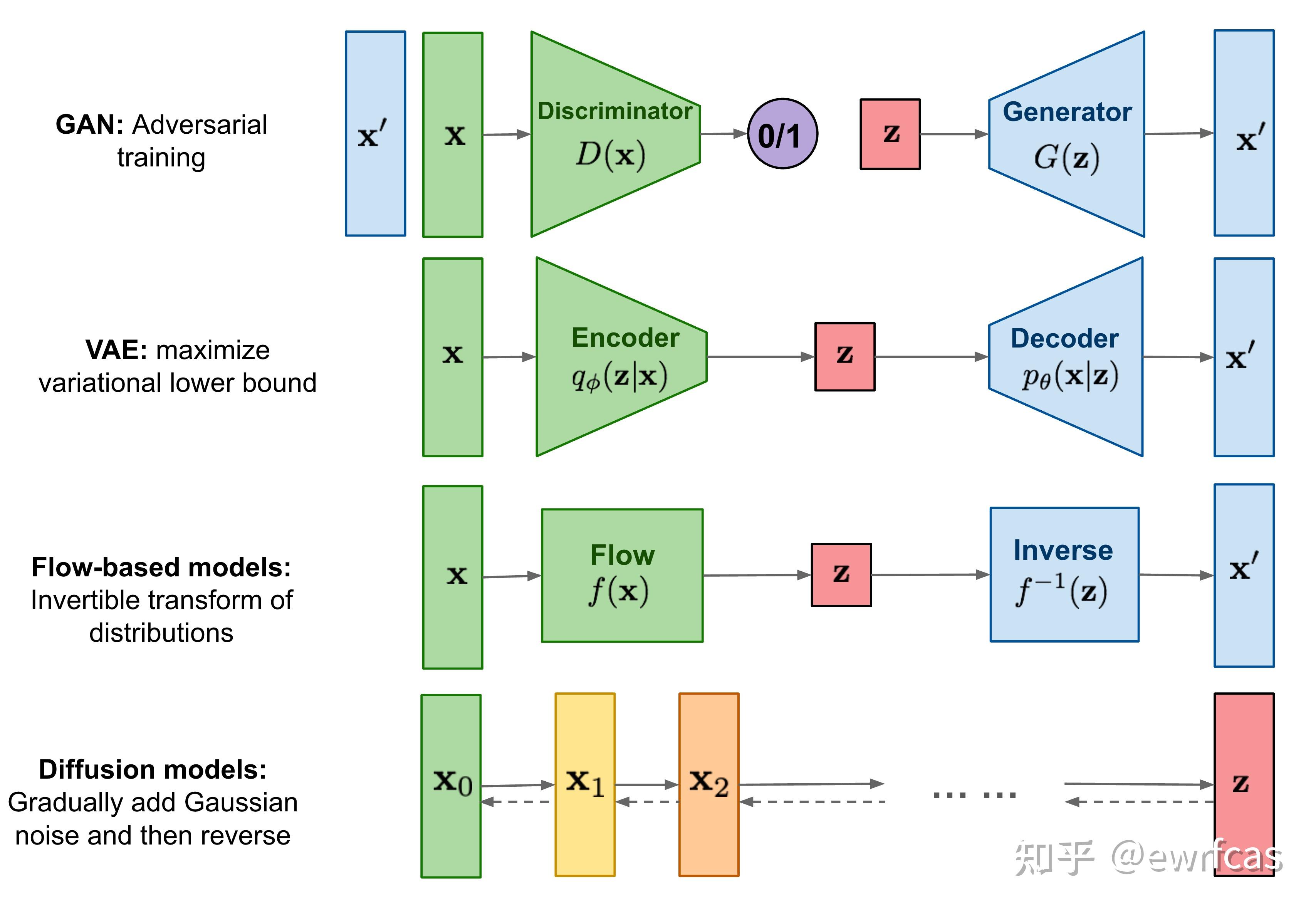
diffusion model和其他模型最大的区别是它的latent code(z)和原图是同尺寸大小的,当然最近也有基于压缩的latent diffusion model,不过是后话了。一句话概括diffusion model,即存在一系列高斯噪声( T 轮),将输入图片 x0 变为纯高斯噪声 xT 。而我们的模型则负责将 xT 复原回图片 x0 。这样一来其实diffusion model和GAN很像,都是给定噪声 xT生成图片 x0 ,但是要强调的是,这里噪声 xT 与图片x0是同维度的。
DDPM
- 线性组合:\(\overline x_t=(1-\lambda)x_0+\lambda x_0'\)
- 前向加噪:\(x'_t~q(x_t|x_0)\)
- 逆向合成:\(\overline x_0~p(x_0|\overline x_t)\)
\(x_t\)是噪声符合高斯分布,\(x_0\)是原始数据。前向不断加噪声获得\(x_t\),反向不断去噪还原\(x_0\)
- 反向去噪需要学习参数\(\theta\)

- ELBO:Evidence Lower Bound
- 想要最大化P(x)
- \(logP(x)=\int_zq_{\phi}(z|x)logP(x)dz\)
- \(=\int_z q_{\phi}(z|x)log(\frac{P(z,x)}{P(z|x)})dz\)
- \(=\int _zq_{\phi}(z|x)log(\frac{P(z,x)}{q_{\phi}(z|x)}\frac{q_{\phi}(z,x)}{P(z|x)})dz\)
- \(=\int_z q_{\phi}(z|x)log(\frac{P(z,x)}{q_{\phi}(z|x)})dz+\int_z q_{\phi}(z|x)log(\frac{q_{\phi}(z,x)}{P(z|x)})dz\)
- \(=\int_z q_{\phi}(z|x)log(\frac{P(z,x)}{q_{\phi}(z|x)})dz+D_{KL}(q_{\phi}(z|x)||P(z|x))\)
- \(log(P(x))\geq \int_z q_{\phi}(z|x)log(\frac{P(z,x)}{q_{\phi}(z|x)})dz=E_{q_{\phi}(z|x)}[log\frac{p(x,z)}{q_{\phi}(z|x)}]\)
- 想要最大化P(x)
- VAE
- \(E_{q_{\phi}(z|x)}[log\frac{p(x,z)}{q_{\phi}(z|x)}]=E_{q_{\phi}(z|x)}[log\ p_{\theta}(x|z)]+E_{q_{\phi}(z|x)}[log\ \frac{p(z)}{q_{\phi}(z|x)}]\)
- \(=E_{q_{\phi}(z|x)}[log\ p_{\theta}(x|z)]-D_{KL}(q_{\phi}(z|x)||p(z))\)
- \(q_{\phi}(z|x)=N(z;\mu_{\phi}(x),\sigma^2_{\phi}(x)I)\)
- \(p(z)=N(z;0,I)\)
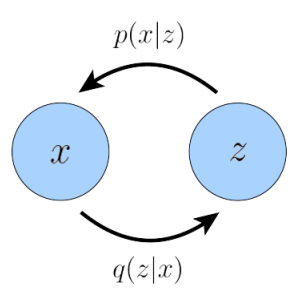
- HVAE
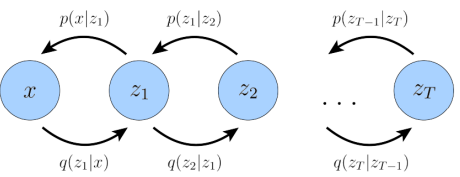
- \(p(x,z_{1:T})=p(z_T)p_{\theta}(x|z_1)\prod_{t=2}^Tp_{\theta}(z_{t-1}|z_t)\)
- \(q_{\phi}(z_{1:T}|x)=q_{\phi}(z_1|x)\prod_{t=2}^Tq_{\phi}(z_t|z_{t-1})\)
- \(log\ p(x)=log \int
p(x,z_{1:T})dz_{1:T}\)
- \(=log \int \frac{p(x,z_{1:T})q_{\phi}(z_{1:T}|x)}{q_{\phi}(z_{1:T}|x)}dz_{1:T}\)
- \(=log\ E_{q_{\phi}(z_{1:T}|x)}[\frac{p(x,z_{1:T})}{q_{\phi}(z_{1:T}|x)}]\)
- \(\geq E_{q_{\phi}(z_{1:T}|x)}[log\ \frac{p(x,z_{1:T})}{q_{\phi}(z_{1:T}|x)}]\)
- \(=E_{q_{\phi}(z_{1:T}|x)}[log\ \frac{p(z_T)p_{\theta}(x|z_1)\prod_{t=2}^Tp_{\theta}(z_{t-1}|z_t)}{q_{\phi}(z_1|x)\prod_{t=2}^Tq_{\phi}(z_t|z_{t-1})}]\)
- 即多次迭代VAE的操作
- Variational Diffusion Models
- \(q(x_{1:T}|x_0)=\prod_{t=1}^Tq(x_t|x_{t-1})\)
- \(q(x_t|x_{t-1})=N(x_t;\sqrt\alpha_t x_{t-1},(1-\alpha_t)I)\)
- \(p(x_{0:T})=p(x_T)\prod_{t=1}^Tp_{\theta}(x_{t-1}|x_t)\)
- \(p(x_T)=N(x_T;0,I)\)
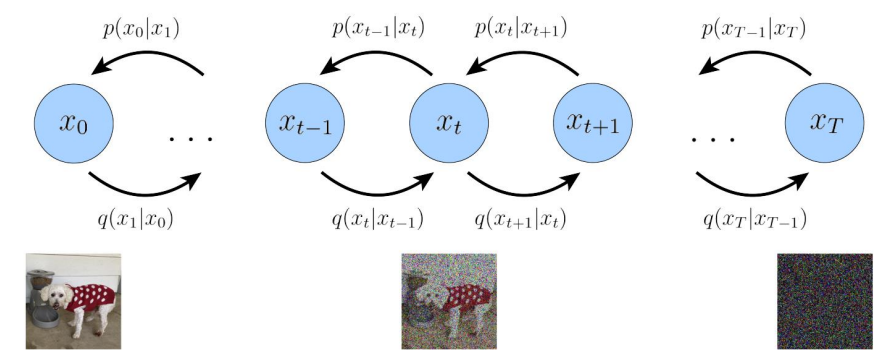
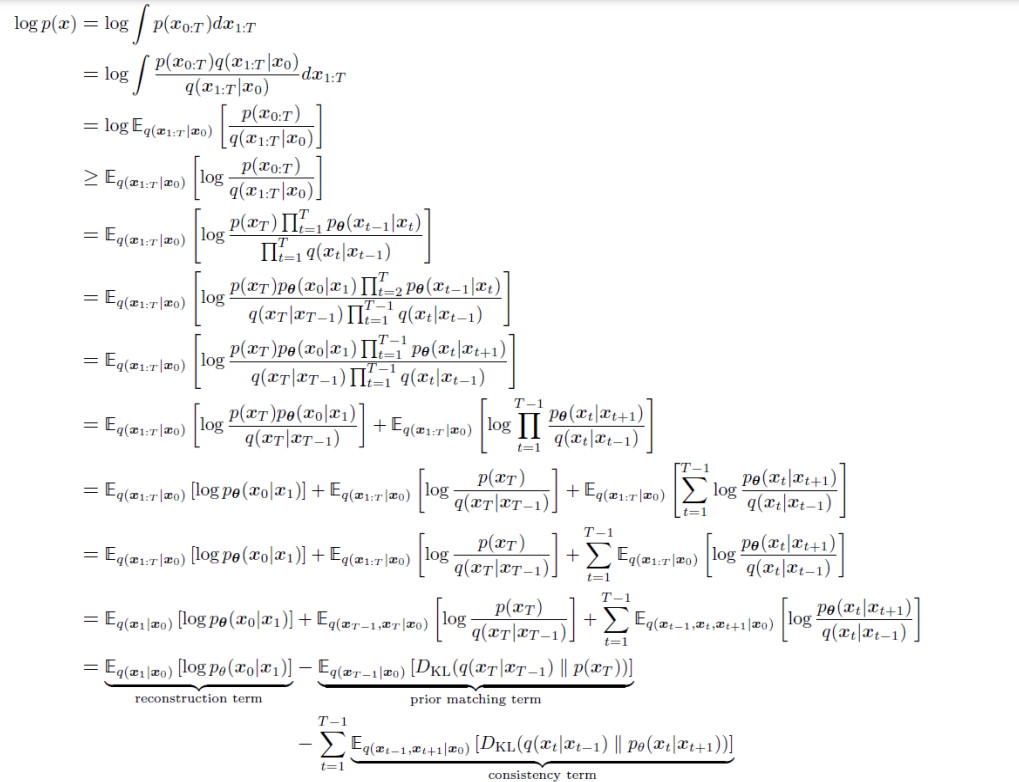
- Diffusion模型的ELBO
[参考blog2][https://blog.csdn.net/Little_White_9/article/details/124435560]
Diffusion扩散过程
所谓前向过程,即往图片上加噪声的过程。虽然这个步骤无法做到图片生成,但是这是理解diffusion model以及构建训练样本GT至关重要的一步。
给定真实图片 \(x_0∼q(x)\) ,diffusion前向过程通过 T 次累计对其添加高斯噪声,得到 \(x_1,x_2,...,x_T\) ,如下图的q过程。这里需要给定一系列的高斯分布方差的超参数$ {t∈(0,1)}{t=1}^T$ .前向过程由于每个时刻 t 只与 t−1 时刻有关,所以也可以看做马尔科夫过程:
- \(q(x_t|x_{t-1})=N(x_t;\sqrt\alpha_t x_{t-1},(1-\alpha_t)I)\)
- \(\beta+\alpha = 1\)
- \(q(x_{1:T}|x_0)=\prod_{t=1}^Tq(x_t|x_{t-1})\)
这个过程中,随着 \(t\) 的增大,$ x_t $越来越接近纯噪声。当 $T→∞ \(,\) x_T$ 是完全的高斯噪声(下面会证明,且与均值系数\(1−β_t\) 的选择有关)。且实际中 βt 随着t增大是递增的,即 $β_1<β_2<...<β_T $。在GLIDE的code中, $β_t $是由0.0001 到0.02线性插值(以 T=1000 为基准, T 增加, β对应降低)。
重参数(reparameterization trick)
重参数技巧在很多工作(gumbel softmax, VAE)中有所引用。如果我们要从某个分布中随机采样(高斯分布)一个样本,这个过程是无法反传梯度的。而这个通过高斯噪声采样得到 \(x_t\) 的过程在diffusion中到处都是,因此我们需要通过重参数技巧来使得他可微。最通常的做法是吧随机性通过一个独立的随机变量( ϵ )引导过去。
举个例子,如果要从高斯分布 $z∼N(z;μ_θ,σ_θ^2I) $采样一个z,我们可以写成:
- \(z=\mu_\theta+\sigma_\theta·\epsilon\)
- \(\epsilon~N(0,I)\)
上式的z依旧是有随机性的, 且满足均值为 \(μ_θ\) 方差为 \(σ_θ^2\) 的高斯分布。这里的\(μ_θ,σ_θ^2\)可以是由参数 θ 的神经网络推断得到的。整个“采样”过程依旧梯度可导,随机性被转嫁到了ϵ上。
任意时刻的 \(x_t\) 可以由 \(x_0\) 和 β 表示
用重参数化技巧表示 \(x_{t}\)
\(x_t=\sqrt\alpha_t x_{t-1}+\sqrt{(1-\alpha_t)}z_{t-1}\)
\(z_t~N(0,I)\)
那么令\(\overline \alpha_t=\prod_{i=1}^t\alpha_i\)
\(x_t=\sqrt{\overline{\alpha_t}}x_0+\frac{\sqrt{\overline{\alpha_t}}}{\sqrt{\overline{\alpha_1}}}\sqrt{1-\alpha_1}z_0+\frac{\sqrt{\overline{\alpha_t}}}{\sqrt{\overline{\alpha_2}}}\sqrt{1-\alpha_2}z_1+\frac{\sqrt{\overline{\alpha_t}}}{\sqrt{\overline{\alpha_3}}}\sqrt{1-\alpha_3}z_2+...+\frac{\sqrt{\overline{\alpha_t}}}{\sqrt{\overline{\alpha_t}}}\sqrt{1-\alpha_t}z_{t-1}\)
设随机变量\(\overline Z_{t-1}\)
\(\overline Z_{t-1}=\frac{\sqrt{\overline{\alpha_t}}}{\sqrt{\overline{\alpha_1}}}\sqrt{1-\alpha_1}z_0+\frac{\sqrt{\overline{\alpha_t}}}{\sqrt{\overline{\alpha_2}}}\sqrt{1-\alpha_2}z_1+\frac{\sqrt{\overline{\alpha_t}}}{\sqrt{\overline{\alpha_3}}}\sqrt{1-\alpha_3}z_2+...+\frac{\sqrt{\overline{\alpha_t}}}{\sqrt{\overline{\alpha_t}}}\sqrt{1-\alpha_t}z_{t-1}\)
- \(E(\overline Z_{t-1})=0\)
- \(D(\overline Z_{t-1})=1-\overline{\alpha_t}\)
\(x_t=\sqrt{\overline{\alpha_t}}x_0+\overline{Z}_{t-1}=\sqrt{\overline{\alpha_t}}x_0+\sqrt{1-\overline{\alpha_t}}Z\)
- \(Z~N(0,I)\)
- \(q(x_t|x_0)=N(x_t;\sqrt{\overline{\alpha_t}}x_0,\sqrt{1-\overline{\alpha_t}}I)\)
至此我们推出了
\(q(x_t|x_{t-1})=N(x_t;\sqrt\alpha_t x_{t-1},(1-\alpha_t)I)\)
\(q(x_t|x_0)=N(x_t;\sqrt{\overline{\alpha_t}}x_0,\sqrt{1-\overline{\alpha_t}}I)\)
如果您喜欢此博客或发现它对您有用,则欢迎对此发表评论。 也欢迎您共享此博客,以便更多人可以参与。 如果博客中使用的图像侵犯了您的版权,请与作者联系以将其删除。 谢谢 !